全一卷
1.函数 的最小值为______.
的最小值为______.
 的最小值为______.
的最小值为______.2.设 ,
, .数列
.数列 的通项公式为
的通项公式为 ______.
______.
 ,
, .数列
.数列 的通项公式为
的通项公式为 ______.
______.3.设平面向量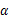 、
、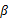 满足
满足 .则
.则 的取值范围是______.
的取值范围是______.
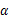 、
、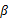 满足
满足 .则
.则 的取值范围是______.
的取值范围是______.4.设 是
是 上具有周期
上具有周期 的奇函数,并且
的奇函数,并且 ,则
,则 在
在 中至少有____个零点.
中至少有____个零点.
 是
是 上具有周期
上具有周期 的奇函数,并且
的奇函数,并且 ,则
,则 在
在 中至少有____个零点.
中至少有____个零点.5.设 为实数,且关于
为实数,且关于 的方程
的方程 有实根.则
有实根.则 的取值范围是______.
的取值范围是______.
 为实数,且关于
为实数,且关于 的方程
的方程 有实根.则
有实根.则 的取值范围是______.
的取值范围是______.6.给定定点 ,动点
,动点 满足线段
满足线段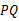 的垂直平分线与抛物线
的垂直平分线与抛物线 相切.则点
相切.则点 的轨迹方程为______.
的轨迹方程为______.
 ,动点
,动点 满足线段
满足线段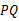 的垂直平分线与抛物线
的垂直平分线与抛物线 相切.则点
相切.则点 的轨迹方程为______.
的轨迹方程为______.7.设 (
( ,
, 为虚数单位),
为虚数单位), 的虚部与
的虚部与 的实部均非负.则满足条件的复平面上的点集
的实部均非负.则满足条件的复平面上的点集 所构成区域的面积为______.
所构成区域的面积为______.
 (
( ,
, 为虚数单位),
为虚数单位), 的虚部与
的虚部与 的实部均非负.则满足条件的复平面上的点集
的实部均非负.则满足条件的复平面上的点集 所构成区域的面积为______.
所构成区域的面积为______.8.设 为正整数.把男女乒乓球选手各
为正整数.把男女乒乓球选手各 人配成男双、女双、混双各
人配成男双、女双、混双各 对,每名选手均不兼项.则配对方式总数为______.
对,每名选手均不兼项.则配对方式总数为______.
 为正整数.把男女乒乓球选手各
为正整数.把男女乒乓球选手各 人配成男双、女双、混双各
人配成男双、女双、混双各 对,每名选手均不兼项.则配对方式总数为______.
对,每名选手均不兼项.则配对方式总数为______.9.设正实数 、
、 满足
满足 ,证明:
,证明: .
.
 、
、 满足
满足 ,证明:
,证明: .
.10.在图1的多面体 中,已知
中,已知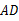 、
、 、
、 均与平面
均与平面 垂直.设
垂直.设 ,
, ,
, ,
, .求四面体
.求四面体 与四面体
与四面体 公共部分的体积(用
公共部分的体积(用 、
、 、
、 表示).
表示).
 中,已知
中,已知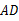 、
、 、
、 均与平面
均与平面 垂直.设
垂直.设 ,
, ,
, ,
, .求四面体
.求四面体 与四面体
与四面体 公共部分的体积(用
公共部分的体积(用 、
、 、
、 表示).
表示).
11.设平面四边形 的四边长为四个连续的正整数.证明:四边形
的四边长为四个连续的正整数.证明:四边形 面积的最大值不为整数.
面积的最大值不为整数.
 的四边长为四个连续的正整数.证明:四边形
的四边长为四个连续的正整数.证明:四边形 面积的最大值不为整数.
面积的最大值不为整数.12.已知31名学生参加了某次考试,考试共有10道题,每名学生至少解出了6道题.证明:存在两名学生,他们解出的题目中至少有5道相同.
 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
