全一卷
1.设 是函数
是函数 的图像上任意一点,过点
的图像上任意一点,过点 分别向直线
分别向直线 和
和 轴作垂线,垂足分别为
轴作垂线,垂足分别为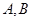 ,则
,则 的值为
的值为__________ .
 是函数
是函数 的图像上任意一点,过点
的图像上任意一点,过点 分别向直线
分别向直线 和
和 轴作垂线,垂足分别为
轴作垂线,垂足分别为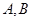 ,则
,则 的值为
的值为2.设 的内角
的内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且满足
,且满足 .则
.则
______ .
 的内角
的内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且满足
,且满足 .则
.则
3.设 、
、 、
、 .则
.则 的最大值是______.
的最大值是______.
 、
、 、
、 .则
.则 的最大值是______.
的最大值是______.4.抛物线 的焦点为
的焦点为 ,准线为
,准线为 ,
, 、
、 是抛物线上的两个动点,且满足
是抛物线上的两个动点,且满足 .设线段
.设线段 的中点
的中点 在
在 上的投影为
上的投影为 ,则
,则 的最大值是( ).
的最大值是( ).
 的焦点为
的焦点为 ,准线为
,准线为 ,
, 、
、 是抛物线上的两个动点,且满足
是抛物线上的两个动点,且满足 .设线段
.设线段 的中点
的中点 在
在 上的投影为
上的投影为 ,则
,则 的最大值是( ).
的最大值是( ).A. | B. | C.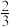 | D. |
5.设同底的两个正三棱锥 和
和 内接于同一个球.若正三棱锥
内接于同一个球.若正三棱锥 的侧面与底面所成的角为
的侧面与底面所成的角为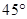 ,则正三棱锥
,则正三棱锥 的侧面与底面所成角的正切值是______.
的侧面与底面所成角的正切值是______.
 和
和 内接于同一个球.若正三棱锥
内接于同一个球.若正三棱锥 的侧面与底面所成的角为
的侧面与底面所成的角为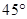 ,则正三棱锥
,则正三棱锥 的侧面与底面所成角的正切值是______.
的侧面与底面所成角的正切值是______.6.设 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当 时,
时, ,若对任意的
,若对任意的 ,不等式
,不等式 恒成立,则实数a的取值范围是
恒成立,则实数a的取值范围是________ .
 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当 时,
时, ,若对任意的
,若对任意的 ,不等式
,不等式 恒成立,则实数a的取值范围是
恒成立,则实数a的取值范围是7.满足 的所有正整数
的所有正整数 的和是______.
的和是______.
 的所有正整数
的所有正整数 的和是______.
的和是______.8.某情报站有 、
、 、
、 、
、 四种互不相同的密码,每周使用其中的一种密码,且每周都是从上周未使用的三种密码中等可能地随机选用一种.设第一周使用
四种互不相同的密码,每周使用其中的一种密码,且每周都是从上周未使用的三种密码中等可能地随机选用一种.设第一周使用 种密码.那么,第七周也使用
种密码.那么,第七周也使用 种密码的概率是______(用最简分数表示).
种密码的概率是______(用最简分数表示).
 、
、 、
、 、
、 四种互不相同的密码,每周使用其中的一种密码,且每周都是从上周未使用的三种密码中等可能地随机选用一种.设第一周使用
四种互不相同的密码,每周使用其中的一种密码,且每周都是从上周未使用的三种密码中等可能地随机选用一种.设第一周使用 种密码.那么,第七周也使用
种密码.那么,第七周也使用 种密码的概率是______(用最简分数表示).
种密码的概率是______(用最简分数表示).9.已知函数 ,其中,
,其中, ,且
,且 .
.
(1)若对任意 ,都有
,都有 ,求
,求 的取值范围.
的取值范围.
(2)若 ,且存在
,且存在 ,使
,使 ,求
,求 的取值范围.
的取值范围.
 ,其中,
,其中, ,且
,且 .
.(1)若对任意
 ,都有
,都有 ,求
,求 的取值范围.
的取值范围.(2)若
 ,且存在
,且存在 ,使
,使 ,求
,求 的取值范围.
的取值范围.10.已知数列 的各项均为非零实数,且对于任意的正整数
的各项均为非零实数,且对于任意的正整数 都有
都有 .
.
(1)当 时,求所有满足条件的三项组成的数列
时,求所有满足条件的三项组成的数列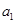 ,
,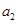 ,
,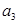 .
.
(2)是否存在满足条件的无穷数列 ,使得
,使得 若存在,求出这样的无穷数列的一个通项公式;若不存在,说明理由.
若存在,求出这样的无穷数列的一个通项公式;若不存在,说明理由.
 的各项均为非零实数,且对于任意的正整数
的各项均为非零实数,且对于任意的正整数 都有
都有 .
.(1)当
 时,求所有满足条件的三项组成的数列
时,求所有满足条件的三项组成的数列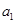 ,
,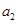 ,
,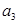 .
.(2)是否存在满足条件的无穷数列
 ,使得
,使得 若存在,求出这样的无穷数列的一个通项公式;若不存在,说明理由.
若存在,求出这样的无穷数列的一个通项公式;若不存在,说明理由.11.如图,在平面直角坐标系 中,菱形
中,菱形 的边长为4,且
的边长为4,且 .
.
(1)证明: 为定值;
为定值;
(2)当点 在半圆
在半圆 :
: 上运动时,求点
上运动时,求点 的轨迹.
的轨迹.
 中,菱形
中,菱形 的边长为4,且
的边长为4,且 .
.(1)证明:
 为定值;
为定值;(2)当点
 在半圆
在半圆 :
: 上运动时,求点
上运动时,求点 的轨迹.
的轨迹.
12.如图,在锐角 中,
中, ,
, 、
、 是边
是边 上不同的两点,使得
上不同的两点,使得 .设
.设 和
和 的外心分别为
的外心分别为 、
、 .证明:
.证明: 、
、 、
、 三点共线.
三点共线.
 中,
中, ,
, 、
、 是边
是边 上不同的两点,使得
上不同的两点,使得 .设
.设 和
和 的外心分别为
的外心分别为 、
、 .证明:
.证明: 、
、 、
、 三点共线.
三点共线.
13.试证明:集合 满足
满足
(1)对每个 及
及 ,若
,若 ,则
,则 一定不是
一定不是 的倍数;
的倍数;
(2)对每个 (
( 表示
表示 在
在 中的补集),且
中的补集),且 ,必存在
,必存在 ,
, ,使
,使 是
是 的倍数.
的倍数.
 满足
满足(1)对每个
 及
及 ,若
,若 ,则
,则 一定不是
一定不是 的倍数;
的倍数;(2)对每个
 (
( 表示
表示 在
在 中的补集),且
中的补集),且 ,必存在
,必存在 ,
, ,使
,使 是
是 的倍数.
的倍数.14.设 是平面上
是平面上 个点,其两两间的距离的最小值为
个点,其两两间的距离的最小值为 .证明:
.证明: .
.
 是平面上
是平面上 个点,其两两间的距离的最小值为
个点,其两两间的距离的最小值为 .证明:
.证明: .
.15.设 (
( 是正整数).证明:对满足
是正整数).证明:对满足 的任意实数
的任意实数 、
、 ,数列
,数列 中有无穷多项属于
中有无穷多项属于 (
(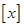 表示不超过实数
表示不超过实数 的最大整数).
的最大整数).
 (
( 是正整数).证明:对满足
是正整数).证明:对满足 的任意实数
的任意实数 、
、 ,数列
,数列 中有无穷多项属于
中有无穷多项属于 (
(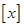 表示不超过实数
表示不超过实数 的最大整数).
的最大整数). 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
