全一卷
1.在平行六面体 中,M为
中,M为 与
与 的交点,若
的交点,若 ,
, ,则与
,则与 相等的向量是( )
相等的向量是( )

 中,M为
中,M为 与
与 的交点,若
的交点,若 ,
, ,则与
,则与 相等的向量是( )
相等的向量是( )
A. | B. | C. | D. |
2.等差数列 中,
中, 是前
是前 项和,且
项和,且 ,
, .则
.则 为( ).
为( ).
 中,
中, 是前
是前 项和,且
项和,且 ,
, .则
.则 为( ).
为( ).| A.2 | B.11 | C.4 | D.12 |
3.已知点 在直线
在直线 上运动,点
上运动,点 、
、 满足
满足 取得最大值.则点
取得最大值.则点 的坐标是( ).
的坐标是( ).
 在直线
在直线 上运动,点
上运动,点 、
、 满足
满足 取得最大值.则点
取得最大值.则点 的坐标是( ).
的坐标是( ).A. | B. | C. | D. |
4.已知 ,对一切
,对一切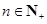 都成立.那么,
都成立.那么, 、
、 、
、 的值为( ).
的值为( ).
 ,对一切
,对一切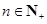 都成立.那么,
都成立.那么, 、
、 、
、 的值为( ).
的值为( ).A. , , | B. |
C. , , | D.不存在这样的 、 、 、 、 |
5.已知 是
是 上的增函数,
上的增函数, 、
、 是其图像上的两个点.那么,
是其图像上的两个点.那么, 的解集的补集是( ).
的解集的补集是( ).
 是
是 上的增函数,
上的增函数, 、
、 是其图像上的两个点.那么,
是其图像上的两个点.那么, 的解集的补集是( ).
的解集的补集是( ).A. | B. |
C. | D. |
6.设数列 满足
满足 ,且
,且 .则数列
.则数列 的前11项的和
的前11项的和 .
.
 满足
满足 ,且
,且 .则数列
.则数列 的前11项的和
的前11项的和 .
.| A.198 | B.55 | C.204 | D.188 |
7.已知 是
是 内一点,且满足
内一点,且满足 .则点
.则点 是
是 的______ .
的______ .
 是
是 内一点,且满足
内一点,且满足 .则点
.则点 是
是 的______ .
的______ .8.若圆锥曲线 的焦距与实数
的焦距与实数 无关,则它的焦点坐标是
无关,则它的焦点坐标是______ .
 的焦距与实数
的焦距与实数 无关,则它的焦点坐标是
无关,则它的焦点坐标是9.设点 、
、 、
、 .则
.则 的形状为______ .
的形状为______ .
 、
、 、
、 .则
.则 的形状为______ .
的形状为______ .10.设直线 ,
, 和
和 有公共点 .则
有公共点 .则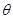 的取值范围是______ .
的取值范围是______ .
 ,
, 和
和 有公共点 .则
有公共点 .则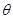 的取值范围是______ .
的取值范围是______ .11.过半径为 5 的球面上的一点 作三条两两垂直的弦
作三条两两垂直的弦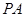 、
、 、
、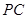 , 且满足
, 且满足 .则
.则 的最大值是______.
的最大值是______.
 作三条两两垂直的弦
作三条两两垂直的弦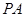 、
、 、
、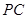 , 且满足
, 且满足 .则
.则 的最大值是______.
的最大值是______.12.设 .则
.则 的最小值是______ .
的最小值是______ .
 .则
.则 的最小值是______ .
的最小值是______ .13.(1)已知 及
及 .求
.求 的值.
的值.
(2)已知 .求
.求 的值 .
的值 .
 及
及 .求
.求 的值.
的值.(2)已知
 .求
.求 的值 .
的值 .14.如图,四棱锥 的底面是正方形,
的底面是正方形, ,
,  , 点
, 点 、
、 分别在棱
分别在棱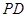 、
、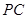 上,且
上,且 .
.

(1)求证 : ;
;
(2)求二面角 的大小;
的大小;
(3)求直线 与平面
与平面 所成角的大小.
所成角的大小.
 的底面是正方形,
的底面是正方形, ,
,  , 点
, 点 、
、 分别在棱
分别在棱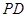 、
、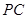 上,且
上,且 .
.
(1)求证 :
 ;
;(2)求二面角
 的大小;
的大小;(3)求直线
 与平面
与平面 所成角的大小.
所成角的大小.15.如图,在平面直角坐标系中,长度为 6的线段 的一个端点
的一个端点 在射线
在射线 上滑动 , 另一个端点
上滑动 , 另一个端点 在射线
在射线 上滑动,点
上滑动,点 在线段
在线段 上 , 且 P
上 , 且 P .
.

(1)求点 的轨迹方程;
的轨迹方程;
(2)若点 的轨迹与
的轨迹与 轴 、
轴 、 轴分别交于点
轴分别交于点 、
、 , 求四边形
, 求四边形 面积的最大值(其中
面积的最大值(其中 是坐标原点).
是坐标原点).
 的一个端点
的一个端点 在射线
在射线 上滑动 , 另一个端点
上滑动 , 另一个端点 在射线
在射线 上滑动,点
上滑动,点 在线段
在线段 上 , 且 P
上 , 且 P .
.
(1)求点
 的轨迹方程;
的轨迹方程;(2)若点
 的轨迹与
的轨迹与 轴 、
轴 、 轴分别交于点
轴分别交于点 、
、 , 求四边形
, 求四边形 面积的最大值(其中
面积的最大值(其中 是坐标原点).
是坐标原点).16.如图,设
 是曲线
是曲线 :
: 上的
上的 个点.点
个点.点 在
在 轴的正半轴上,满足
轴的正半轴上,满足 是正三角形(
是正三角形( 是坐标原点).
是坐标原点).

(1)求点 的横坐标
的横坐标 关于
关于 的表达式;
的表达式;
(2)试求 的值.
的值.
( 表示这个数的整数部分,当
表示这个数的整数部分,当 时,取
时,取 ;当
;当 时 ,
时 ,  .
. .)
.)

 是曲线
是曲线 :
: 上的
上的 个点.点
个点.点 在
在 轴的正半轴上,满足
轴的正半轴上,满足 是正三角形(
是正三角形( 是坐标原点).
是坐标原点).
(1)求点
 的横坐标
的横坐标 关于
关于 的表达式;
的表达式;(2)试求
 的值.
的值.(
 表示这个数的整数部分,当
表示这个数的整数部分,当 时,取
时,取 ;当
;当 时 ,
时 ,  .
. .)
.) 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
