全一卷
1.已知 是一等差数列,
是一等差数列, 是其前
是其前 项之和. 则
项之和. 则 是
是 ,
, 的( )条件.
的( )条件.
 是一等差数列,
是一等差数列, 是其前
是其前 项之和. 则
项之和. 则 是
是 ,
, 的( )条件.
的( )条件.| A.充分必要 | B.充分而不必要 |
| C.必要而不充分 | D.既不充分也不必要 |
2.已知函数 在其定义域内既有极大值又有极小值. 则实数
在其定义域内既有极大值又有极小值. 则实数 的取值范围是( )
的取值范围是( )
 在其定义域内既有极大值又有极小值. 则实数
在其定义域内既有极大值又有极小值. 则实数 的取值范围是( )
的取值范围是( )A. | B. |
C. | D. 或 或 |
3.若集合 和集合
和集合 满足
满足 ,则实数
,则实数 的取值范围是( ).
的取值范围是( ).
 和集合
和集合 满足
满足 ,则实数
,则实数 的取值范围是( ).
的取值范围是( ).A. | B. |
C. | D. |
4.已知 ,
, ,
, . 则
. 则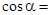 .
.
 ,
, ,
, . 则
. 则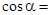 .
.A. | B. | C. | D. |
5.已知整数集合 ,集合
,集合 满足条件:(1)
满足条件:(1) ;(2)若
;(2)若 ,则
,则 ,则所有这样的集合
,则所有这样的集合 的个数为( ).
的个数为( ).
 ,集合
,集合 满足条件:(1)
满足条件:(1) ;(2)若
;(2)若 ,则
,则 ,则所有这样的集合
,则所有这样的集合 的个数为( ).
的个数为( ).| A.15 | B.16 | C.31 | D.32 |
6.已知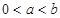 ,在
,在 、
、 之间插入一个正数
之间插入一个正数 ,使
,使 、
、 、
、 成等比数列;在
成等比数列;在 、
、 之间插入两个正数
之间插入两个正数 、
、 ,使
,使 、
、 、
、 、
、 成等差数列. 则
成等差数列. 则 与
与 的大小关系为( ).
的大小关系为( ).
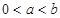 ,在
,在 、
、 之间插入一个正数
之间插入一个正数 ,使
,使 、
、 、
、 成等比数列;在
成等比数列;在 、
、 之间插入两个正数
之间插入两个正数 、
、 ,使
,使 、
、 、
、 、
、 成等差数列. 则
成等差数列. 则 与
与 的大小关系为( ).
的大小关系为( ).A. |
B. |
C. |
| D.不确定 |
7.设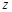 为复数,
为复数, 为虚数单位. 若
为虚数单位. 若 ,
, ,则当
,则当 ,为实数时,
,为实数时, 的最小值为( ).
的最小值为( ).
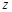 为复数,
为复数, 为虚数单位. 若
为虚数单位. 若 ,
, ,则当
,则当 ,为实数时,
,为实数时, 的最小值为( ).
的最小值为( ).A. | B.3 | C.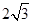 | D. |
8.在多项式 的展开式中,每一字母的指数均不为零的项共有( )项.
的展开式中,每一字母的指数均不为零的项共有( )项.
 的展开式中,每一字母的指数均不为零的项共有( )项.
的展开式中,每一字母的指数均不为零的项共有( )项.| A.35 | B.42 | C.45 | D.50 |
9.如图,在三棱锥 中,侧面
中,侧面 底面
底面 ,底面
,底面 是边长为1的正三角形,
是边长为1的正三角形, ,
, ,
, 是棱
是棱 的中点. 则
的中点. 则 与
与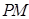 间的距离为( ).
间的距离为( ).

 中,侧面
中,侧面 底面
底面 ,底面
,底面 是边长为1的正三角形,
是边长为1的正三角形, ,
, ,
, 是棱
是棱 的中点. 则
的中点. 则 与
与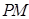 间的距离为( ).
间的距离为( ).
A. | B. | C. | D. |
10.某人从上一层到二层需跨10级台阶. 他一步可能跨1级台阶,称为一阶步,也可能跨2级台阶,称为二阶步,最多能跨3级台阶,称为三阶步. 从一层上到二层他总共跨了6步,而且任何相邻两步均不同阶. 则他从一层到二层可能的不同过程共有( )种.
| A.6 | B.8 | C.10 | D.12 |
11.已知函数 ,若在任何长度为2的闭区间上总存在两点
,若在任何长度为2的闭区间上总存在两点 、
、 ,使
,使 成立,则
成立,则 的最小值为______.
的最小值为______.
 ,若在任何长度为2的闭区间上总存在两点
,若在任何长度为2的闭区间上总存在两点 、
、 ,使
,使 成立,则
成立,则 的最小值为______.
的最小值为______.12.已知 的垂心为
的垂心为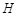 . 若
. 若 ,
, ,且点
,且点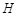 在圆
在圆 上移动,则动点
上移动,则动点 的轨迹为______.
的轨迹为______.
 的垂心为
的垂心为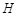 . 若
. 若 ,
, ,且点
,且点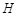 在圆
在圆 上移动,则动点
上移动,则动点 的轨迹为______.
的轨迹为______.13.若函数 ,则
,则 ______.
______.
 ,则
,则 ______.
______.14.函数 的图像的对称中心为______.
的图像的对称中心为______.
 的图像的对称中心为______.
的图像的对称中心为______.15.如图,在三棱锥 中,
中, ,
, ,
, . 若此三棱锥的体积为定值
. 若此三棱锥的体积为定值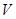 ,求点
,求点 到平面
到平面 距离的最大值.
距离的最大值.
 中,
中, ,
, ,
, . 若此三棱锥的体积为定值
. 若此三棱锥的体积为定值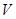 ,求点
,求点 到平面
到平面 距离的最大值.
距离的最大值.
16.已知 、
、 是椭圆
是椭圆 的左、右焦点,弦
的左、右焦点,弦 经过点
经过点 ,且
,且 ,
, .
.
(1)求椭圆的离心率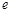 ;
;
(2)若 的面积为2,求椭圆的方程.
的面积为2,求椭圆的方程.
 、
、 是椭圆
是椭圆 的左、右焦点,弦
的左、右焦点,弦 经过点
经过点 ,且
,且 ,
, .
.(1)求椭圆的离心率
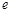 ;
;(2)若
 的面积为2,求椭圆的方程.
的面积为2,求椭圆的方程.17.已知函数 对于任意实数
对于任意实数 、
、 ,都有
,都有 ,且当
,且当 时,
时, .
.
(1) 在实数集
在实数集 上是否为单调函数?并说明理由;
上是否为单调函数?并说明理由;
(2)若 ,求
,求 .
.
 对于任意实数
对于任意实数 、
、 ,都有
,都有 ,且当
,且当 时,
时, .
.(1)
 在实数集
在实数集 上是否为单调函数?并说明理由;
上是否为单调函数?并说明理由;(2)若
 ,求
,求 .
.18.服装销售商甲和乙欲销某品牌服装制造企业生产的服装. 该企业的设计部门在无任何有关甲和乙销售信息的情况下,随机地为他们提供了 种不同设计的款式,由甲和乙各自独立地选定自己认可的那些款式. 则至少有一个款式为甲和乙共同认可的概率为多少?
种不同设计的款式,由甲和乙各自独立地选定自己认可的那些款式. 则至少有一个款式为甲和乙共同认可的概率为多少?
 种不同设计的款式,由甲和乙各自独立地选定自己认可的那些款式. 则至少有一个款式为甲和乙共同认可的概率为多少?
种不同设计的款式,由甲和乙各自独立地选定自己认可的那些款式. 则至少有一个款式为甲和乙共同认可的概率为多少?19.某年级 位同学参加语文和数学两门课的考试,每门课的考分从0到100分. 假如考试的结果没有两位同学的成绩是完全相同的(即至少有一门课的成绩不同). 另外,“甲比乙好”是指同学甲的语文和数学的考分均分别高于同学乙的语文和数学的考分. 试问:当
位同学参加语文和数学两门课的考试,每门课的考分从0到100分. 假如考试的结果没有两位同学的成绩是完全相同的(即至少有一门课的成绩不同). 另外,“甲比乙好”是指同学甲的语文和数学的考分均分别高于同学乙的语文和数学的考分. 试问:当 最小为何值时,必存在三位同学(设为甲、乙、丙),有甲比乙好,乙比丙好.
最小为何值时,必存在三位同学(设为甲、乙、丙),有甲比乙好,乙比丙好.
 位同学参加语文和数学两门课的考试,每门课的考分从0到100分. 假如考试的结果没有两位同学的成绩是完全相同的(即至少有一门课的成绩不同). 另外,“甲比乙好”是指同学甲的语文和数学的考分均分别高于同学乙的语文和数学的考分. 试问:当
位同学参加语文和数学两门课的考试,每门课的考分从0到100分. 假如考试的结果没有两位同学的成绩是完全相同的(即至少有一门课的成绩不同). 另外,“甲比乙好”是指同学甲的语文和数学的考分均分别高于同学乙的语文和数学的考分. 试问:当 最小为何值时,必存在三位同学(设为甲、乙、丙),有甲比乙好,乙比丙好.
最小为何值时,必存在三位同学(设为甲、乙、丙),有甲比乙好,乙比丙好. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
