全一卷
1.随机抛掷三个大小、质地相同的正方体色子.在三个色子所示数字中最小值是3的概率为_____
2.关于x的方程 有模为3的虚数根.则实数a的值为_______.
有模为3的虚数根.则实数a的值为_______.
 有模为3的虚数根.则实数a的值为_______.
有模为3的虚数根.则实数a的值为_______.3.已知正项数列 的首项为1,且对于一切正整数n,均有
的首项为1,且对于一切正整数n,均有 则
则 _____.
_____.
 的首项为1,且对于一切正整数n,均有
的首项为1,且对于一切正整数n,均有 则
则 _____.
_____.4.设以 、
、 为焦点的椭圆的离心率为e,以
为焦点的椭圆的离心率为e,以 为顶点、
为顶点、 为焦点的抛物线与椭圆的一个交点为P,若
为焦点的抛物线与椭圆的一个交点为P,若 ,则e的值为________.
,则e的值为________.
 、
、 为焦点的椭圆的离心率为e,以
为焦点的椭圆的离心率为e,以 为顶点、
为顶点、 为焦点的抛物线与椭圆的一个交点为P,若
为焦点的抛物线与椭圆的一个交点为P,若 ,则e的值为________.
,则e的值为________.5.设实数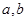 满足
满足 ,且
,且 ,则
,则 的最大值为________.
的最大值为________.
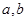 满足
满足 ,且
,且 ,则
,则 的最大值为________.
的最大值为________.6.函数 的值域为________.
的值域为________.
 的值域为________.
的值域为________.7.正四凌锥P-ABCD外接于一个半径为1的球面,若球心到四凌锥各个面的距离相等,则此四凌锥的底面面积为________.
8.设△ABC的外心为O,内心为I,∠B=45°.若OI∥BC,则cosC的值为_________.
9.设等比数列 和
和 ,记
,记 .
.
(1)写出一组 、
、 、
、 和
和 、
、 、
、 ,使得
,使得 、
、 、
、 是公差不为0的等差数列;
是公差不为0的等差数列;
(2)当 时,证明:
时,证明: 不可能是公差不为0的等差数列.
不可能是公差不为0的等差数列.
 和
和 ,记
,记 .
.(1)写出一组
 、
、 、
、 和
和 、
、 、
、 ,使得
,使得 、
、 、
、 是公差不为0的等差数列;
是公差不为0的等差数列;(2)当
 时,证明:
时,证明: 不可能是公差不为0的等差数列.
不可能是公差不为0的等差数列.10.在平面直角坐标系 中,已知椭圆:
中,已知椭圆: 的右焦点为F,过点F的直线l与椭圆C交于A、B两点,试问:在x轴上是否存在定点P,使得当直线l绕点F旋转时,均有
的右焦点为F,过点F的直线l与椭圆C交于A、B两点,试问:在x轴上是否存在定点P,使得当直线l绕点F旋转时,均有 为定值?
为定值?
 中,已知椭圆:
中,已知椭圆: 的右焦点为F,过点F的直线l与椭圆C交于A、B两点,试问:在x轴上是否存在定点P,使得当直线l绕点F旋转时,均有
的右焦点为F,过点F的直线l与椭圆C交于A、B两点,试问:在x轴上是否存在定点P,使得当直线l绕点F旋转时,均有 为定值?
为定值?11.设多项式 .若对于任意的非负实数x、y,有
.若对于任意的非负实数x、y,有 求a、b、c所满足的条件.
求a、b、c所满足的条件.
 .若对于任意的非负实数x、y,有
.若对于任意的非负实数x、y,有 求a、b、c所满足的条件.
求a、b、c所满足的条件.12.如图,E、F分别为△ABC、△ACDA 的内心,AC 平分∠BAD, ,延长EC,与△BCE的外接圆交于点R,若RK∥EF,证明:A为△BCD的外心.
,延长EC,与△BCE的外接圆交于点R,若RK∥EF,证明:A为△BCD的外心.
 ,延长EC,与△BCE的外接圆交于点R,若RK∥EF,证明:A为△BCD的外心.
,延长EC,与△BCE的外接圆交于点R,若RK∥EF,证明:A为△BCD的外心.
13.求所有的正整数n,使得对于任意正实数a、b、c满足a+b+c=1,有

14.设n为正整数.求满足以下条件的三元正整数组(a、b、c)的个数:
(ⅰ)ab=n;
(ⅱ) ;
;
(ⅲ)a、b、c的最大公约数为1.
(ⅰ)ab=n;
(ⅱ)
 ;
;(ⅲ)a、b、c的最大公约数为1.
15.设a、b、c、d、e为正实数,且 ,若五个正三角形的面积分别为
,若五个正三角形的面积分别为 ,证明:这五个三角形中存在四个能覆盖面积为1的正△ABC.
,证明:这五个三角形中存在四个能覆盖面积为1的正△ABC.
 ,若五个正三角形的面积分别为
,若五个正三角形的面积分别为 ,证明:这五个三角形中存在四个能覆盖面积为1的正△ABC.
,证明:这五个三角形中存在四个能覆盖面积为1的正△ABC. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
