全一卷
1.设 是非负整数,满足
是非负整数,满足 .则
.则 ______.
______.
 是非负整数,满足
是非负整数,满足 .则
.则 ______.
______.2.已知 ,函数
,函数 和
和 的图像交于点
的图像交于点 ,且它们分别与
,且它们分别与 轴交于点
轴交于点 、
、 .若
.若 的面积是1,则
的面积是1,则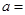 ______.
______.
 ,函数
,函数 和
和 的图像交于点
的图像交于点 ,且它们分别与
,且它们分别与 轴交于点
轴交于点 、
、 .若
.若 的面积是1,则
的面积是1,则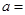 ______.
______.3.已知 是公差为正数
是公差为正数 的等差数列的前
的等差数列的前 项之和.若
项之和.若 在
在 时取到最小值,则
时取到最小值,则 的取值范围是
的取值范围是______ .
 是公差为正数
是公差为正数 的等差数列的前
的等差数列的前 项之和.若
项之和.若 在
在 时取到最小值,则
时取到最小值,则 的取值范围是
的取值范围是4.已知函数 在
在 的切线与
的切线与 轴交于点
轴交于点 .若
.若 ,
, ,则
,则 ______.
______.
 在
在 的切线与
的切线与 轴交于点
轴交于点 .若
.若 ,
, ,则
,则 ______.
______.5.函数 对于一切
对于一切 、
、 、
、 满足
满足 .则
.则 ______.
______.
 对于一切
对于一切 、
、 、
、 满足
满足 .则
.则 ______.
______.6.在锐角 中,设
中,设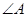 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 .若
.若 ,则
,则 的最小值是______.
的最小值是______.
 中,设
中,设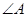 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 .若
.若 ,则
,则 的最小值是______.
的最小值是______.7.已知 是椭圆
是椭圆 上的一动点,
上的一动点, 、
、 是椭圆的两个焦点.则
是椭圆的两个焦点.则 的取值范围是
的取值范围是______ .
 是椭圆
是椭圆 上的一动点,
上的一动点, 、
、 是椭圆的两个焦点.则
是椭圆的两个焦点.则 的取值范围是
的取值范围是8.用三种颜色给立方体的八个顶点染色,其中至少有一种颜色恰好染四个顶点.则任一条棱的两个端点都不同色的概率是______.
9.已知 ,
, .求
.求 的值.
的值.
 ,
, .求
.求 的值.
的值.10.设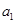 ,
,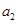 ,…,
,…, 是1,2,…,
是1,2,…, 的一个排列.求证:
的一个排列.求证: .
.
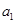 ,
,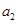 ,…,
,…, 是1,2,…,
是1,2,…, 的一个排列.求证:
的一个排列.求证: .
.11.对任意的正整数 ,证明:
,证明: .
.
 ,证明:
,证明: .
.12.设 是一些互不相同的四元数组
是一些互不相同的四元数组 的集合,其中,
的集合,其中, 或
或 .已知
.已知 的元素个数不超过15,且满足:若
的元素个数不超过15,且满足:若 、
、 ,则
,则 、
、 ,其中,
,其中, ,
, .求集合
.求集合 元素个数的最大值.
元素个数的最大值.
 是一些互不相同的四元数组
是一些互不相同的四元数组 的集合,其中,
的集合,其中, 或
或 .已知
.已知 的元素个数不超过15,且满足:若
的元素个数不超过15,且满足:若 、
、 ,则
,则 、
、 ,其中,
,其中, ,
, .求集合
.求集合 元素个数的最大值.
元素个数的最大值. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
