全一卷
1.若 是
是 上周期为5的奇函数,且满足
上周期为5的奇函数,且满足 ,则
,则 .
.
 是
是 上周期为5的奇函数,且满足
上周期为5的奇函数,且满足 ,则
,则 .
.| A.6 | B.7 | C.8 | D.9 |
2.对于非零向量 有两个命题.
有两个命题.
命题甲: ;
;
命题乙:函数 为一次函数.
为一次函数.
则甲是乙的条件.
 有两个命题.
有两个命题.命题甲:
 ;
;命题乙:函数
 为一次函数.
为一次函数.则甲是乙的条件.
| A.充分不必要 |
| B.必要不充分 |
| C.充分必要 |
| D.既不充分也不必要 |
3.如图,若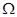 是长方体ABCD-A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是
是长方体ABCD-A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是

 是长方体ABCD-A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是
是长方体ABCD-A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是
| A.EH∥FG | B.四边形EFGH是矩形 |
C.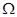 是棱柱 是棱柱 | D.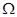 是棱台 是棱台 |
4.如图,在半径为 的圆内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形,如此无限继续下去,设
的圆内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形,如此无限继续下去,设 为前
为前 个圆的面积之和. 取正数
个圆的面积之和. 取正数 . 若
. 若 ,则
,则 的取值为.
的取值为.

 的圆内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形,如此无限继续下去,设
的圆内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形,如此无限继续下去,设 为前
为前 个圆的面积之和. 取正数
个圆的面积之和. 取正数 . 若
. 若 ,则
,则 的取值为.
的取值为.
| A.大于100的所有自然数 |
| B.大于100的有限个自然数 |
| C.不大于100的所有自然数 |
| D.不大于100的有限个自然数 |
5.设直线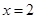 与双曲线
与双曲线 的渐近线交于点
的渐近线交于点 、
、 ,记
,记 ,
, ,任取双曲线
,任取双曲线 上的点
上的点 . 若
. 若 ,则.
,则.
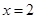 与双曲线
与双曲线 的渐近线交于点
的渐近线交于点 、
、 ,记
,记 ,
, ,任取双曲线
,任取双曲线 上的点
上的点 . 若
. 若 ,则.
,则.A. |
B. |
C. |
D. |
6.一厂家有一批长40cm、宽30cm的矩形红布. 现该厂家要将每块矩形红布剪一次后拼成一面三角形旗子. 则红布可以拼成三角形旗子的种数是.
| A.1 | B.2 | C.3 | D.4 |
7.设定义在区间 上的函数
上的函数 的图象与
的图象与 的图象交于点P,过点P作x轴的垂线,垂足为
的图象交于点P,过点P作x轴的垂线,垂足为 ,直线
,直线 与函数
与函数 的图象交于点
的图象交于点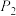 ,则线段
,则线段 的长为
的长为________ .
 上的函数
上的函数 的图象与
的图象与 的图象交于点P,过点P作x轴的垂线,垂足为
的图象交于点P,过点P作x轴的垂线,垂足为 ,直线
,直线 与函数
与函数 的图象交于点
的图象交于点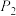 ,则线段
,则线段 的长为
的长为8.在等比数列 中,
中, ,
, ,函数
,函数 .
.
则函数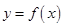 在点
在点 处的切线方程为______.
处的切线方程为______.
 中,
中, ,
, ,函数
,函数 .
.则函数
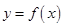 在点
在点 处的切线方程为______.
处的切线方程为______.9.如果执行图所示的程序,输入正整数 、
、 ,那么,输出的
,那么,输出的 等于______.
等于______.
 、
、 ,那么,输出的
,那么,输出的 等于______.
等于______.
10.已知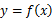 为区间
为区间 上的连续函数,且恒有
上的连续函数,且恒有 ,可以用随机模拟方法近似计算积分
,可以用随机模拟方法近似计算积分 . 先产生两组(每组
. 先产生两组(每组 个)区间
个)区间 上的均匀随机数
上的均匀随机数 和
和 ,由此得到
,由此得到 个点
个点 ;再数出其中满足
;再数出其中满足 的点数
的点数 . 那么,由随机模拟方法可得积分
. 那么,由随机模拟方法可得积分 的近似值为______.
的近似值为______.
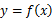 为区间
为区间 上的连续函数,且恒有
上的连续函数,且恒有 ,可以用随机模拟方法近似计算积分
,可以用随机模拟方法近似计算积分 . 先产生两组(每组
. 先产生两组(每组 个)区间
个)区间 上的均匀随机数
上的均匀随机数 和
和 ,由此得到
,由此得到 个点
个点 ;再数出其中满足
;再数出其中满足 的点数
的点数 . 那么,由随机模拟方法可得积分
. 那么,由随机模拟方法可得积分 的近似值为______.
的近似值为______.11.设 是
是 的二项展开式中
的二项展开式中 的系数. 则
的系数. 则 ______.
______.
 是
是 的二项展开式中
的二项展开式中 的系数. 则
的系数. 则 ______.
______.12.若三个非零的实数 成等比数列,则其公比是______.
成等比数列,则其公比是______.
 成等比数列,则其公比是______.
成等比数列,则其公比是______.13.设函数 .若
.若 成立的充分条件是
成立的充分条件是 ,则实数
,则实数 的取值范围是______.
的取值范围是______.
 .若
.若 成立的充分条件是
成立的充分条件是 ,则实数
,则实数 的取值范围是______.
的取值范围是______.14.空间有五个点,任意四点不共面. 若连了若干条线段而图中不存在四面体,则图中三角形个数的最大值为______.
15.已知当 时,不等式
时,不等式 恒成立. 试求实数
恒成立. 试求实数 的取值范围.
的取值范围.
 时,不等式
时,不等式 恒成立. 试求实数
恒成立. 试求实数 的取值范围.
的取值范围.16.如图, 、
、 在
在 内滚动且始终保持与
内滚动且始终保持与 内切,切点分别为
内切,切点分别为 、
、 ,
, 是
是 和
和 的外公切线. 已知
的外公切线. 已知 、
、 、
、 的半径分别为
的半径分别为 、
、 、
、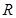 . 求证:
. 求证: 为定值.
为定值.
 、
、 在
在 内滚动且始终保持与
内滚动且始终保持与 内切,切点分别为
内切,切点分别为 、
、 ,
, 是
是 和
和 的外公切线. 已知
的外公切线. 已知 、
、 、
、 的半径分别为
的半径分别为 、
、 、
、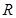 . 求证:
. 求证: 为定值.
为定值.
17.设椭圆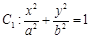 ,
, ,过原点
,过原点 引射线分别与椭圆
引射线分别与椭圆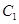 、
、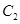 交于点
交于点 、
、 ,
, 为线段
为线段 上一点.
上一点.
(1)求证: 、
、 、
、 成等比数列的充要条件点
成等比数列的充要条件点 的轨迹方程为
的轨迹方程为 .
.
(2)试利用合情推理,将(1)的结论类比到双曲线得出相应的正确结论(不要求证明).
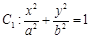 ,
, ,过原点
,过原点 引射线分别与椭圆
引射线分别与椭圆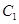 、
、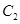 交于点
交于点 、
、 ,
, 为线段
为线段 上一点.
上一点.(1)求证:
 、
、 、
、 成等比数列的充要条件点
成等比数列的充要条件点 的轨迹方程为
的轨迹方程为 .
.(2)试利用合情推理,将(1)的结论类比到双曲线得出相应的正确结论(不要求证明).
18.设 是整数1,2,…,
是整数1,2,…, 的一个排列,且满足
的一个排列,且满足
(1) ;
;
(2) .
.
记上述排列的个数为 . 试求
. 试求 被3除的余数.
被3除的余数.
 是整数1,2,…,
是整数1,2,…, 的一个排列,且满足
的一个排列,且满足(1)
 ;
;(2)
 .
.记上述排列的个数为
 . 试求
. 试求 被3除的余数.
被3除的余数. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
