全一卷
1.已知 为偶函数,且
为偶函数,且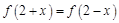 ,当
,当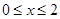 时,
时,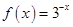 .若
.若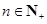 ,
,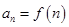 ,则
,则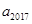 等于.
等于.
 为偶函数,且
为偶函数,且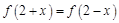 ,当
,当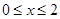 时,
时,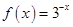 .若
.若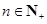 ,
,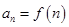 ,则
,则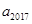 等于.
等于.| A.27 | B.3 | C. | D. |
2.从集合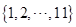 中任取两个元素作为椭圆方程
中任取两个元素作为椭圆方程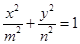 中的m、n.则能组成落在矩形区域
中的m、n.则能组成落在矩形区域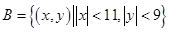 内的椭圆的个数是.
内的椭圆的个数是.
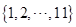 中任取两个元素作为椭圆方程
中任取两个元素作为椭圆方程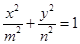 中的m、n.则能组成落在矩形区域
中的m、n.则能组成落在矩形区域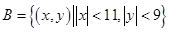 内的椭圆的个数是.
内的椭圆的个数是.| A.43 | B.72 | C.86 | D.9 |
3.函数 的图像大致是图中的.
的图像大致是图中的.
 的图像大致是图中的.
的图像大致是图中的.A. | B. |
C. | D. |
4.设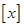 表示不超过x的最大整数,Z表示整数集,方程
表示不超过x的最大整数,Z表示整数集,方程 的解集为M,则有.
的解集为M,则有.
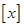 表示不超过x的最大整数,Z表示整数集,方程
表示不超过x的最大整数,Z表示整数集,方程 的解集为M,则有.
的解集为M,则有.A. | B. |
C. | D.M与Z互不包含 |
5.已知不等式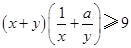 对于任意正实数x、y恒成立.则正实数a的最小值为().
对于任意正实数x、y恒成立.则正实数a的最小值为().
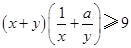 对于任意正实数x、y恒成立.则正实数a的最小值为().
对于任意正实数x、y恒成立.则正实数a的最小值为().| A.2 | B.4 | C.6 | D.8 |
6.A、B两位同学各有3张卡片,现以投掷均匀硬币的形式进行游戏.当出现正面向上时,A赢得B—张卡片,否则,B赢得A—张卡片.若某人已赢得所有卡片,则游戏终止.那么,恰好掷完5次硬币时游戏终止的概率是.
A. | B. | C. | D. |
7.在△ABC中,角A、B、C的对边分别为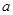 、
、 、
、 ,且
,且 ,则角B的大小是 _________.
,则角B的大小是 _________.
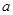 、
、 、
、 ,且
,且 ,则角B的大小是 _________.
,则角B的大小是 _________.8.掷一次硬币,出现正面与背面的概率都是 .当第n次投掷出现正面时,令
.当第n次投掷出现正面时,令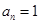 ;当第n次投掷出现背面时,令
;当第n次投掷出现背面时,令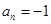 .又记
.又记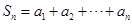 ,则
,则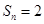 的概率是
的概率是____ .
 .当第n次投掷出现正面时,令
.当第n次投掷出现正面时,令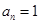 ;当第n次投掷出现背面时,令
;当第n次投掷出现背面时,令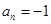 .又记
.又记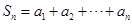 ,则
,则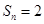 的概率是
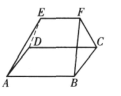
的概率是9.如图.在多面体ABCDEF中,已知四边形ABCD是边长为3的正方形,EF∥AB, .若该多面体的体积为
.若该多面体的体积为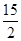 ,则
,则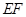 与AC的距离为
与AC的距离为____ .
 .若该多面体的体积为
.若该多面体的体积为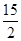 ,则
,则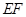 与AC的距离为
与AC的距离为
10.给定平面上的五个点A、B、C、D、E,任意三点不共线.由这些点连成4条线,每点至少是一条线段的端点,不同的联结方式有____ 种.
11.已知 ,
,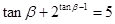 .则
.则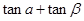 等于
等于____ .
 ,
,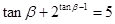 .则
.则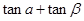 等于
等于12.已知双曲线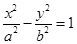 的左顶点为A,右焦点为
的左顶点为A,右焦点为
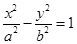 的左顶点为A,右焦点为
的左顶点为A,右焦点为A.设P为第一象限中双曲线上的任意一点.若总有 ,则双曲线的离心率e等于________. ,则双曲线的离心率e等于________. |
13.在数列 中,已知
中,已知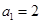 ,
,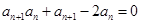 对于任意正整数n,有
对于任意正整数n,有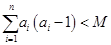 (M为常数,且为整数).求M的最小值.
(M为常数,且为整数).求M的最小值.
 中,已知
中,已知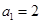 ,
,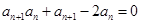 对于任意正整数n,有
对于任意正整数n,有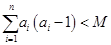 (M为常数,且为整数).求M的最小值.
(M为常数,且为整数).求M的最小值.14.设顶点为P的抛物线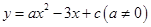 交x轴正半轴于点A、B交y轴正半轴于点C,
交x轴正半轴于点A、B交y轴正半轴于点C,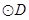 过A、B、C三点,恰好与y轴相切.求证:PA丄DA.
过A、B、C三点,恰好与y轴相切.求证:PA丄DA.
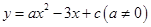 交x轴正半轴于点A、B交y轴正半轴于点C,
交x轴正半轴于点A、B交y轴正半轴于点C, 过A、B、C三点,恰好与y轴相切.求证:PA丄DA.
过A、B、C三点,恰好与y轴相切.求证:PA丄DA.15.已知数列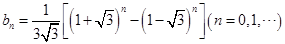 .
.
(1)n是什么数时,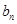 是整数?
是整数?
(2)如果n是奇数,并且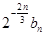 是整数,那么,n是多少?
是整数,那么,n是多少?
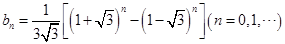 .
.(1)n是什么数时,
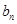 是整数?
是整数?(2)如果n是奇数,并且
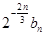 是整数,那么,n是多少?
是整数,那么,n是多少?16.如图,在梯形ABCD中,AD∥BC,BC=BD=1,AB=AC,CD<1,且∠BAC+∠BDC=180°.求CD的长.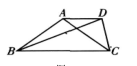

17.已知n为正整数.求证: 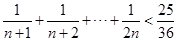 .
.
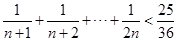 .
.18.如图,依顺时针方向,从1开始,走1步到2,再走2步到3,最后走3步到4.对于大于1的自然数n,能否将1至n排在圆周上,使得从1开始,走一步到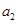 ,再走
,再走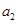 步到
步到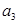 ,……最后,走
,……最后,走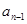 步到
步到 ?这里
?这里 是1,2,1…,n的一个排列.
是1,2,1…,n的一个排列.
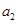 ,再走
,再走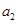 步到
步到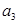 ,……最后,走
,……最后,走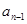 步到
步到 ?这里
?这里 是1,2,1…,n的一个排列.
是1,2,1…,n的一个排列. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
