全一卷
1.“ ,
, ”为“曲线
”为“曲线 经过点
经过点 ”的条件.
”的条件.
 ,
, ”为“曲线
”为“曲线 经过点
经过点 ”的条件.
”的条件.| A.充分不必要 | B.必要不充分 |
| C.充分必要 | D.既不充分也不必要 |
2.已知一个角大于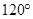 的三角形的三边长分别为
的三角形的三边长分别为 、
、 、
、 . 则实数
. 则实数 的取值范围是.
的取值范围是.
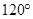 的三角形的三边长分别为
的三角形的三边长分别为 、
、 、
、 . 则实数
. 则实数 的取值范围是.
的取值范围是.A. | B. |
C. | D. |
3.如图1,在正方体 中,已知
中,已知 为
为 的中点. 则二面角
的中点. 则二面角 的余弦值为.
的余弦值为.

 中,已知
中,已知 为
为 的中点. 则二面角
的中点. 则二面角 的余弦值为.
的余弦值为.
A. | B. | C. | D. |
4.若实数 、
、 满足
满足 则
则 的最大值为.
的最大值为.
 、
、 满足
满足 则
则 的最大值为.
的最大值为.| A.1 | B. | C. | D.2 |
5.已知等腰 的三个顶点分别在等腰
的三个顶点分别在等腰 的三条边上. 则
的三条边上. 则 的最小值为.
的最小值为.
 的三个顶点分别在等腰
的三个顶点分别在等腰 的三条边上. 则
的三条边上. 则 的最小值为.
的最小值为.A. | B. | C. | D. |
6.已知数列 的通项
的通项 .若
.若 ,则实数
,则实数 的值为
的值为
 的通项
的通项 .若
.若 ,则实数
,则实数 的值为
的值为A. | B. | C. | D. |
7.若过点 ,
, ,
, ,
, 作四条直线构成一个正方形,则该正方形的面积不可能等于.
作四条直线构成一个正方形,则该正方形的面积不可能等于.
 ,
, ,
, ,
, 作四条直线构成一个正方形,则该正方形的面积不可能等于.
作四条直线构成一个正方形,则该正方形的面积不可能等于.A. | B. | C. | D. |
8.若集合 ,则集合
,则集合 中的元素个数为.
中的元素个数为.
 ,则集合
,则集合 中的元素个数为.
中的元素个数为.| A.4030 | B.4032 |
C. | D. |
9.已知函数 满足
满足 ,
, ,且
,且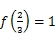 .则
.则 ______.
______.
 满足
满足 ,
, ,且
,且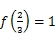 .则
.则 ______.
______.10.若数列 的前
的前 项和
项和 ,则
,则 ______.
______.
 的前
的前 项和
项和 ,则
,则 ______.
______.11.已知点 ,
, 为抛物线
为抛物线 的焦点,
的焦点, 为抛物线上的动点.当
为抛物线上的动点.当 取最小值,点
取最小值,点 的坐标为______.
的坐标为______.
 ,
, 为抛物线
为抛物线 的焦点,
的焦点, 为抛物线上的动点.当
为抛物线上的动点.当 取最小值,点
取最小值,点 的坐标为______.
的坐标为______.12.若 ,则
,则 ______.
______.
 ,则
,则 ______.
______.13.设函数 ,其中,
,其中, 表示
表示 、
、 、
、 中的最小者.若
中的最小者.若 ,则实数
,则实数 的取值范围是
的取值范围是______ .
 ,其中,
,其中, 表示
表示 、
、 、
、 中的最小者.若
中的最小者.若 ,则实数
,则实数 的取值范围是
的取值范围是14.设向量 、
、 的夹角为
的夹角为 ,向量
,向量 、
、 的夹角为
的夹角为 ,
, ,
, .则
.则 的最大值为
的最大值为______ .
 、
、 的夹角为
的夹角为 ,向量
,向量 、
、 的夹角为
的夹角为 ,
, ,
, .则
.则 的最大值为
的最大值为15.设 、
、 .若对任意的
.若对任意的 ,均有
,均有 ,则
,则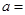
______ ,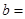
______ .
 、
、 .若对任意的
.若对任意的 ,均有
,均有 ,则
,则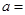
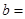
16.设 、
、 ,函数
,函数 .若对任意实数
.若对任意实数 ,方程
,方程 有两个相异的实根,求实数
有两个相异的实根,求实数 的取值范围.
的取值范围.
 、
、 ,函数
,函数 .若对任意实数
.若对任意实数 ,方程
,方程 有两个相异的实根,求实数
有两个相异的实根,求实数 的取值范围.
的取值范围.17.已知椭圆 的离心率为
的离心率为 ,右焦点为圆
,右焦点为圆 的圆心.
的圆心.
(1)求椭圆 的方程;
的方程;
(2)若直线 与曲线
与曲线 、
、 各只有一个公共点,记直线
各只有一个公共点,记直线 与圆
与圆 的公共点为
的公共点为 ,求点
,求点 的坐标.
的坐标.
 的离心率为
的离心率为 ,右焦点为圆
,右焦点为圆 的圆心.
的圆心.(1)求椭圆
 的方程;
的方程;(2)若直线
 与曲线
与曲线 、
、 各只有一个公共点,记直线
各只有一个公共点,记直线 与圆
与圆 的公共点为
的公共点为 ,求点
,求点 的坐标.
的坐标.18.已知数列 、
、 满足
满足 ,
, ,
, .证明:
.证明: .
.
 、
、 满足
满足 ,
, ,
, .证明:
.证明: .
.19.已知数列 满足
满足 ,
, .
.
(1)证明: 为正整数数列;
为正整数数列;
(2)是否存在 ,使得
,使得 ?并说明理由.
?并说明理由.
 满足
满足 ,
, .
.(1)证明:
 为正整数数列;
为正整数数列;(2)是否存在
 ,使得
,使得 ?并说明理由.
?并说明理由.20.设 为正整数.若数字
为正整数.若数字 构成的排列
构成的排列 满足
满足
(1) ;
;
(2) ;
;
(3) ,
,
则称此排列为“N型”的.记 为所有N型排列的个数.
为所有N型排列的个数.
(1)求 、
、 的值;
的值;
(2)证明:对任意正整数 ,
, 均为奇数.
均为奇数.
 为正整数.若数字
为正整数.若数字 构成的排列
构成的排列 满足
满足(1)
 ;
;(2)
 ;
;(3)
 ,
,则称此排列为“N型”的.记
 为所有N型排列的个数.
为所有N型排列的个数.(1)求
 、
、 的值;
的值;(2)证明:对任意正整数
 ,
, 均为奇数.
均为奇数. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
