全一卷
1.设 、
、 、
、 为三个集合.则“
为三个集合.则“ 、
、 均为
均为 的子集”是
的子集”是 成立的( )条件
成立的( )条件
 、
、 、
、 为三个集合.则“
为三个集合.则“ 、
、 均为
均为 的子集”是
的子集”是 成立的( )条件
成立的( )条件| A.充分不必要 | B.必要不充分 | C.充分必要 | D.既不充分也不必要 |
2.方程 表示的曲线为( )
表示的曲线为( )
 表示的曲线为( )
表示的曲线为( )| A.一个圆 | B.两个半圆 | C.一个椭圆 | D.以上结论均不对 |
3.用 表示不超过实数
表示不超过实数 的最大整数.则方程
的最大整数.则方程 共有( )个不同的实根.
共有( )个不同的实根.
 表示不超过实数
表示不超过实数 的最大整数.则方程
的最大整数.则方程 共有( )个不同的实根.
共有( )个不同的实根.| A.1 | B.2 | C.3 | D.4 |
4.方程 共有( )个不同的实根.
共有( )个不同的实根.
 共有( )个不同的实根.
共有( )个不同的实根.| A.0 | B.1 | C.2 | D.3 |
5.在正方体的十二条面对角线和四条体对角线随机地选取两条对角线.则这两条对角线所在的直线为异面直线的概率等于( )
A. | B. | C. | D.以上结果均不对 |
6.设 的周长为12,内切圆半径为1.则( )
的周长为12,内切圆半径为1.则( )
 的周长为12,内切圆半径为1.则( )
的周长为12,内切圆半径为1.则( )A. 必为直角三角形 必为直角三角形 | B. 必为锐角三角形 必为锐角三角形 |
C. 必为直角三角形或锐角三角形 必为直角三角形或锐角三角形 | D.以上结论均不对 |
7.在正四棱锥 中,四个侧面均为等边三角形,设该四棱锥的侧面与底面所成的二面角的大小为
中,四个侧面均为等边三角形,设该四棱锥的侧面与底面所成的二面角的大小为 ,则,
,则, __________.
__________.
 中,四个侧面均为等边三角形,设该四棱锥的侧面与底面所成的二面角的大小为
中,四个侧面均为等边三角形,设该四棱锥的侧面与底面所成的二面角的大小为 ,则,
,则, __________.
__________.8.设 、
、 分别为等差数列
分别为等差数列 、
、 的前
的前 项之和.若
项之和.若 ,则
,则 __________.
__________.
 、
、 分别为等差数列
分别为等差数列 、
、 的前
的前 项之和.若
项之和.若 ,则
,则 __________.
__________.9.设 为原点,
为原点, 为抛物线
为抛物线 上的动点,
上的动点, 为抛物线
为抛物线 上的动点.则
上的动点.则 面积的最小值为__________.
面积的最小值为__________.
 为原点,
为原点, 为抛物线
为抛物线 上的动点,
上的动点, 为抛物线
为抛物线 上的动点.则
上的动点.则 面积的最小值为__________.
面积的最小值为__________.10.设 .则
.则 除以100的余数为__________.
除以100的余数为__________.
 .则
.则 除以100的余数为__________.
除以100的余数为__________.11.设复数 .则
.则 的值为
的值为__________ (用数学作答).
 .则
.则 的值为
的值为12.设 、
、 、
、 、
、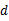 均为实数,满足
均为实数,满足 .则
.则 的最小值为__________.
的最小值为__________.
 、
、 、
、 、
、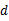 均为实数,满足
均为实数,满足 .则
.则 的最小值为__________.
的最小值为__________.13.设 .证明:对任意的
.证明:对任意的 ,有
,有 .
.
 .证明:对任意的
.证明:对任意的 ,有
,有 .
.14.已知正 内接于抛物线
内接于抛物线 ,
, 的重心
的重心 落在双曲线
落在双曲线 上.求点
上.求点 的坐标.
的坐标.
 内接于抛物线
内接于抛物线 ,
, 的重心
的重心 落在双曲线
落在双曲线 上.求点
上.求点 的坐标.
的坐标.15.设 ,
, ,
, .
.
证明:(1)存在常数 ,使得对任意正整数
,使得对任意正整数 ,有
,有 .
.
(2)对任意正整数 ,有
,有 .
.
 ,
, ,
, .
.证明:(1)存在常数
 ,使得对任意正整数
,使得对任意正整数 ,有
,有 .
.(2)对任意正整数
 ,有
,有 .
. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
