全一卷
1.若 ,则下列不等式不能成立的是( )
,则下列不等式不能成立的是( )
 ,则下列不等式不能成立的是( )
,则下列不等式不能成立的是( )A. | B. | C. | D. |
2.函数 的单调递减区间是( ).
的单调递减区间是( ).
 的单调递减区间是( ).
的单调递减区间是( ).A. | B. | C. | D. |
3.已知集合 ,且满足
,且满足 中任何2个元素的和都不能被5整除.则集合
中任何2个元素的和都不能被5整除.则集合 中元素的个数最多是( )个.
中元素的个数最多是( )个.
 ,且满足
,且满足 中任何2个元素的和都不能被5整除.则集合
中任何2个元素的和都不能被5整除.则集合 中元素的个数最多是( )个.
中元素的个数最多是( )个.| A.10 | B.11 | C.12 | D.13 |
4.已知 .则
.则 与1的大小关系是( ).
与1的大小关系是( ).
 .则
.则 与1的大小关系是( ).
与1的大小关系是( ).A. | B. |
C. | D.大小与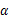 的取值有关 的取值有关 |
5.如图,正方体 —
— 的侧面
的侧面 内有一点
内有一点 到两直线
到两直线 、
、 的距离相等.那么,
的距离相等.那么, 的轨迹是.
的轨迹是.

 —
— 的侧面
的侧面 内有一点
内有一点 到两直线
到两直线 、
、 的距离相等.那么,
的距离相等.那么, 的轨迹是.
的轨迹是.
| A.抛物线的一部分 | B.双曲线的一部分 |
| C.椭圆的一部分 | D.线段 |
6.已知 ,
, ,且
,且 ,点
,点 满足
满足 ,
, ,
, .则
.则 是.
是.
 ,
, ,且
,且 ,点
,点 满足
满足 ,
, ,
, .则
.则 是.
是.A. | B. |
C. | D. |
7.如果 、
、 、
、 是三角形的三边长,且满足
是三角形的三边长,且满足 ,则这个三角形的形状是______.
,则这个三角形的形状是______.
 、
、 、
、 是三角形的三边长,且满足
是三角形的三边长,且满足 ,则这个三角形的形状是______.
,则这个三角形的形状是______.8.一个数列的各项均为3或5,首项为3,且在第 个3和第
个3和第 个3之间有
个3之间有 个5,即3,5,3,5,5,3,5,5,5,5,3,….则此数列的前2004项的和
个5,即3,5,3,5,5,3,5,5,5,5,3,….则此数列的前2004项的和 =______.
=______.
 个3和第
个3和第 个3之间有
个3之间有 个5,即3,5,3,5,5,3,5,5,5,5,3,….则此数列的前2004项的和
个5,即3,5,3,5,5,3,5,5,5,5,3,….则此数列的前2004项的和 =______.
=______.9.设直线 与抛物线
与抛物线 相交于
相交于 、
、 两点,
两点, 为坐标原点.则当
为坐标原点.则当 的面积最大时,直线
的面积最大时,直线 的方程为______.
的方程为______.
 与抛物线
与抛物线 相交于
相交于 、
、 两点,
两点, 为坐标原点.则当
为坐标原点.则当 的面积最大时,直线
的面积最大时,直线 的方程为______.
的方程为______.10.一个正三棱锥的三条侧棱长均为1,且两两垂直.将这个三棱锥绕着它的高旋转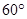 ,则旋转后的三棱锥与原三棱锥公共部分的体积为
,则旋转后的三棱锥与原三棱锥公共部分的体积为______ .
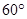 ,则旋转后的三棱锥与原三棱锥公共部分的体积为
,则旋转后的三棱锥与原三棱锥公共部分的体积为11.某校盖教学楼,需甲种尺寸的玻璃400块,乙种尺寸的玻璃500块.商店中有 、
、 两种规格的玻璃.已知
两种规格的玻璃.已知 种规格的玻璃每块48元,可裁成甲、乙两种尺寸的玻璃分别为4块和6块;
种规格的玻璃每块48元,可裁成甲、乙两种尺寸的玻璃分别为4块和6块; 种规格的玻璃每块58元,可裁成甲、乙两种尺寸的玻璃各为5块.则该校购买
种规格的玻璃每块58元,可裁成甲、乙两种尺寸的玻璃各为5块.则该校购买 、
、 两种规格的玻璃所付出的最少费用是______元.
两种规格的玻璃所付出的最少费用是______元.
 、
、 两种规格的玻璃.已知
两种规格的玻璃.已知 种规格的玻璃每块48元,可裁成甲、乙两种尺寸的玻璃分别为4块和6块;
种规格的玻璃每块48元,可裁成甲、乙两种尺寸的玻璃分别为4块和6块; 种规格的玻璃每块58元,可裁成甲、乙两种尺寸的玻璃各为5块.则该校购买
种规格的玻璃每块58元,可裁成甲、乙两种尺寸的玻璃各为5块.则该校购买 、
、 两种规格的玻璃所付出的最少费用是______元.
两种规格的玻璃所付出的最少费用是______元.12.已知 且方程
且方程 恰有两解.则实数
恰有两解.则实数 的取值范围是______.
的取值范围是______.
 且方程
且方程 恰有两解.则实数
恰有两解.则实数 的取值范围是______.
的取值范围是______.13.已知 在
在 上有意义,
上有意义, ,且满足
,且满足 、
、 时,有
时,有 .
.
(1)数列 满足
满足 .设
.设 ,求
,求 的通项公式;
的通项公式;
(2)设 ,求
,求 的值.
的值.
 在
在 上有意义,
上有意义, ,且满足
,且满足 、
、 时,有
时,有 .
.(1)数列
 满足
满足 .设
.设 ,求
,求 的通项公式;
的通项公式;(2)设
 ,求
,求 的值.
的值.14.如图,点 、
、 是四边形
是四边形 的边
的边 、
、 的中点,
的中点, 与
与 相交于点
相交于点 ,
, 与
与 相交于点
相交于点 .求证:
.求证: .
. 
 、
、 是四边形
是四边形 的边
的边 、
、 的中点,
的中点, 与
与 相交于点
相交于点 ,
, 与
与 相交于点
相交于点 .求证:
.求证: .
. 
15.甲、乙两人轮流掷一枚均匀的硬币,谁先掷出正面,谁获胜.他们连玩了数局,并规定前一局的输家下一局先掷.若甲第1局先掷,则第6局甲获胜的概率是多少?
 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
