全一卷
1.已知 则
则 .
.
 则
则 .
.| A.2 | B.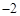 | C. | D. |
2.“ 成等差数列”是“
成等差数列”是“ ”的
”的
 成等差数列”是“
成等差数列”是“ ”的
”的| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
3.若方程 在
在  内有解,则
内有解,则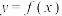 的图象可能是( )
的图象可能是( )
 在
在  内有解,则
内有解,则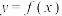 的图象可能是( )
的图象可能是( )A. | B. |
C. | D. |
4.设向量 、
、 的夹角为
的夹角为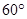 ,且
,且 ,
, .则
.则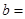 .
.
 、
、 的夹角为
的夹角为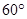 ,且
,且 ,
, .则
.则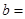 .
.A. | B. | C.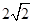 | D.2 |
5.已知 .若对任意的
.若对任意的 有
有 ,则实数
,则实数 的取值范围是.
的取值范围是.
 .若对任意的
.若对任意的 有
有 ,则实数
,则实数 的取值范围是.
的取值范围是.A. | B. |
C. | D. |
6.已知函数 在区间
在区间 上存在最大值.则实数
上存在最大值.则实数 的取值范围是.
的取值范围是.
 在区间
在区间 上存在最大值.则实数
上存在最大值.则实数 的取值范围是.
的取值范围是.A. | B. |
C. | D. |
7.已知四棱锥 的底面是边长为2的正方形,
的底面是边长为2的正方形, 平面
平面 ,且
,且 .则四棱锥
.则四棱锥 的外接球的表面积为______.
的外接球的表面积为______.
 的底面是边长为2的正方形,
的底面是边长为2的正方形, 平面
平面 ,且
,且 .则四棱锥
.则四棱锥 的外接球的表面积为______.
的外接球的表面积为______.8.设数列 的前
的前 项和为
项和为 ,且
,且 .则数列
.则数列 的通项公式为______.
的通项公式为______.
 的前
的前 项和为
项和为 ,且
,且 .则数列
.则数列 的通项公式为______.
的通项公式为______.9.已知函数 的最小正周期为
的最小正周期为 .则
.则 在区间
在区间 上的值域为______.
上的值域为______.
 的最小正周期为
的最小正周期为 .则
.则 在区间
在区间 上的值域为______.
上的值域为______.10.如图所示,在四棱锥 中,底面
中,底面 为正方形,
为正方形, 平面
平面 .已知
.已知 ,
, 为线段
为线段 上的一点,二面角
上的一点,二面角 与二面角
与二面角 的大小相等.则
的大小相等.则 的长为______.
的长为______.
 中,底面
中,底面 为正方形,
为正方形, 平面
平面 .已知
.已知 ,
, 为线段
为线段 上的一点,二面角
上的一点,二面角 与二面角
与二面角 的大小相等.则
的大小相等.则 的长为______.
的长为______.
11.从0,1,…,9中选出三个不同数字组成四位数(其中的一个数字可以出现两次),如5224.则这样的四位数共有______个.
12.非空集合 .当
.当 时,函数
时,函数 既存在最大值,又存在最小值,则实数
既存在最大值,又存在最小值,则实数 的取值范围是______.
的取值范围是______.
 .当
.当 时,函数
时,函数 既存在最大值,又存在最小值,则实数
既存在最大值,又存在最小值,则实数 的取值范围是______.
的取值范围是______.13.在 中,内角
中,内角 、
、 、
、 对边的边长分别为
对边的边长分别为 、
、 、
、 .已知
.已知 ,
, .求:
.求:
(1) 周长的最大值;
周长的最大值;
(2)当 时,
时, 的面积.
的面积.
 中,内角
中,内角 、
、 、
、 对边的边长分别为
对边的边长分别为 、
、 、
、 .已知
.已知 ,
, .求:
.求:(1)
 周长的最大值;
周长的最大值;(2)当
 时,
时, 的面积.
的面积.14.已知椭圆 ,直线
,直线 与椭圆
与椭圆 交于点
交于点 、
、 ,且
,且 .判断直线
.判断直线 与
与 的位置关系,并给出证明.
的位置关系,并给出证明.
 ,直线
,直线 与椭圆
与椭圆 交于点
交于点 、
、 ,且
,且 .判断直线
.判断直线 与
与 的位置关系,并给出证明.
的位置关系,并给出证明.15.已知对任意的 ,均有
,均有 .求实数
.求实数 的取值范围.
的取值范围.
 ,均有
,均有 .求实数
.求实数 的取值范围.
的取值范围.16.已知 ,设实数
,设实数 、
、 、
、 、
、 、
、 、
、 满足
满足
(i) 、
、 、
、 且不全为0;
且不全为0;
(ii) 、
、 、
、 ;
;
(iii)若 ,则
,则 .
.
若所有形如 和
和 的数均不为2014的倍数,则称集合
的数均不为2014的倍数,则称集合 为“好集”.求好集
为“好集”.求好集 所含元素个数的最大值.
所含元素个数的最大值.
 ,设实数
,设实数 、
、 、
、 、
、 、
、 、
、 满足
满足(i)
 、
、 、
、 且不全为0;
且不全为0;(ii)
 、
、 、
、 ;
;(iii)若
 ,则
,则 .
.若所有形如
 和
和 的数均不为2014的倍数,则称集合
的数均不为2014的倍数,则称集合 为“好集”.求好集
为“好集”.求好集 所含元素个数的最大值.
所含元素个数的最大值. 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
