全一卷
1.复数 等于
等于
 等于
等于A. | B. | C. | D. |
2.设集合 ,
, ,则
,则 等于
等于
 ,
, ,则
,则 等于
等于A.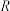 | B. | C. | D. |
3.若抛物线 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 的值为
的值为
 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 的值为
的值为A.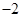 | B. | C. | D.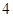 |
4.设 ,已知命题
,已知命题 ;命题
;命题 ,则
,则 是
是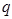 成立的
成立的
 ,已知命题
,已知命题 ;命题
;命题 ,则
,则 是
是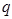 成立的
成立的| A.必要不充分条件 | B.充分不必要条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
5.函数 的反函数是()
的反函数是()
 的反函数是()
的反函数是()A. | B. | C. | D. |
6.将函数 的图象按向量
的图象按向量 平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是
平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是

 的图象按向量
的图象按向量 平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是
平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是
A. |
B. |
C. |
D. |
7.若曲线 的一条切线
的一条切线 与直线
与直线 垂直,则
垂直,则 的方程为
的方程为
 的一条切线
的一条切线 与直线
与直线 垂直,则
垂直,则 的方程为
的方程为A. |
B. |
C. |
D. |
8.设 ,对于函数
,对于函数 ,下列结论正确的是
,下列结论正确的是
 ,对于函数
,对于函数 ,下列结论正确的是
,下列结论正确的是| A.有最大值而无最小值 |
| B.有最小值而无最大值 |
| C.有最大值且有最小值 |
| D.既无最大值又无最小值 |
9.表面积为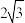 的正八面体的各个顶点都在同一个球面上,则此球的体积为
的正八面体的各个顶点都在同一个球面上,则此球的体积为
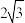 的正八面体的各个顶点都在同一个球面上,则此球的体积为
的正八面体的各个顶点都在同一个球面上,则此球的体积为A. | B. | C. | D. |
10.如果实数 满足条件
满足条件 ,那么
,那么 的最大值为( )
的最大值为( )
 满足条件
满足条件 ,那么
,那么 的最大值为( )
的最大值为( )A. | B. | C. | D. |
11.如果 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于 的三个内角的正弦值,则
的三个内角的正弦值,则
 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于 的三个内角的正弦值,则
的三个内角的正弦值,则A. 和 和 都是锐角三角形 都是锐角三角形 |
B. 和 和 都是钝角三角形 都是钝角三角形 |
C. 是钝角三角形, 是钝角三角形, 是锐角三角形 是锐角三角形 |
D. 是锐角三角形, 是锐角三角形, 是钝角三角形 是钝角三角形 |
12.在正方体上任选3个顶点连成三角形,则所得的三角形是直角非等腰三角形的概率为
A.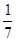 | B. | C.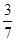 | D. |
13.设常数 ,
, 展开式中
展开式中 的系数为
的系数为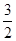 ,则
,则
__________ .
 ,
, 展开式中
展开式中 的系数为
的系数为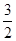 ,则
,则
14.在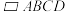 中,
中, ,M为BC的中点,则
,M为BC的中点,则 _______.(用
_______.(用 表示)
表示)
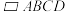 中,
中, ,M为BC的中点,则
,M为BC的中点,则 _______.(用
_______.(用 表示)
表示)15.函数 对于任意实数
对于任意实数 满足条件
满足条件 ,若
,若 则
则
_______________ .
 对于任意实数
对于任意实数 满足条件
满足条件 ,若
,若 则
则
16.多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点 在平面
在平面 内,其余顶点在
内,其余顶点在 的同侧,正方体上与顶点
的同侧,正方体上与顶点 相邻的三个顶点到
相邻的三个顶点到 的距离分别为1,2和4,
的距离分别为1,2和4, 是正方体的其余四个顶点中的一个,则
是正方体的其余四个顶点中的一个,则 到平面
到平面 的距离可能是:
的距离可能是:
①3; ②4; ③5; ④6; ⑤7
以上结论正确的为________________________ .(写出所有正确结论的编号)

 在平面
在平面 内,其余顶点在
内,其余顶点在 的同侧,正方体上与顶点
的同侧,正方体上与顶点 相邻的三个顶点到
相邻的三个顶点到 的距离分别为1,2和4,
的距离分别为1,2和4, 是正方体的其余四个顶点中的一个,则
是正方体的其余四个顶点中的一个,则 到平面
到平面 的距离可能是:
的距离可能是:①3; ②4; ③5; ④6; ⑤7
以上结论正确的为

17.已知
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的值.
的值.

(Ⅰ)求
 的值;
的值;(Ⅱ)求
 的值.
的值.18.(本大题满分12分)在添加剂的搭配使用中,为了找到最佳的搭配方案,需要对各种不同的搭配方式作比较。在试制某种牙膏新品种时,需要选用两种不同的添加剂。现有芳香度分别为0,1,2,3,4,5的六种添加剂可供选用。根据试验设计原理,通常首先要随机选取两种不同的添加剂进行搭配试验。用 表示所选用的两种不同的添加剂的芳香度之和。
表示所选用的两种不同的添加剂的芳香度之和。
(Ⅰ)写出 的分布列;(以列表的形式给出结论,不必写计算过程)
的分布列;(以列表的形式给出结论,不必写计算过程)
(Ⅱ)求 的数学期望
的数学期望 。(要求写出计算过程或说明道理)
。(要求写出计算过程或说明道理)
 表示所选用的两种不同的添加剂的芳香度之和。
表示所选用的两种不同的添加剂的芳香度之和。(Ⅰ)写出
 的分布列;(以列表的形式给出结论,不必写计算过程)
的分布列;(以列表的形式给出结论,不必写计算过程)(Ⅱ)求
 的数学期望
的数学期望 。(要求写出计算过程或说明道理)
。(要求写出计算过程或说明道理)19.(本大题满分12分)如图,P是边长为1的正六边形ABCDEF所在平面外一点, ,P在平面ABC内的射影为BF的中点O。
,P在平面ABC内的射影为BF的中点O。
(Ⅰ)证明 ⊥
⊥ ;
;
(Ⅱ)求面 与面
与面 所成二面角的大小。
所成二面角的大小。
 ,P在平面ABC内的射影为BF的中点O。
,P在平面ABC内的射影为BF的中点O。(Ⅰ)证明
 ⊥
⊥ ;
;(Ⅱ)求面
 与面
与面 所成二面角的大小。
所成二面角的大小。
20.(本大题满分12分)已知函数 在R上有定义,对任何实数
在R上有定义,对任何实数 和任何实数
和任何实数 ,都有
,都有
(Ⅰ)证明 ;(Ⅱ)证明
;(Ⅱ)证明 其中
其中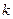 和
和 均为常数;
均为常数;
(Ⅲ)当(Ⅱ)中的 时,设
时,设 ,讨论
,讨论 在
在 内的单调性并求极值
内的单调性并求极值
 在R上有定义,对任何实数
在R上有定义,对任何实数 和任何实数
和任何实数 ,都有
,都有
(Ⅰ)证明
 ;(Ⅱ)证明
;(Ⅱ)证明 其中
其中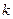 和
和 均为常数;
均为常数;(Ⅲ)当(Ⅱ)中的
 时,设
时,设 ,讨论
,讨论 在
在 内的单调性并求极值
内的单调性并求极值21.(本大题满分12分)数列 的前
的前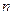 项和为
项和为 ,已知
,已知
(Ⅰ)写出 与
与 的递推关系式
的递推关系式 ,并求
,并求 关于
关于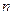 的表达式;
的表达式;
(Ⅱ)设 ,求数列
,求数列 的前
的前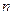 项和
项和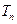 。
。
 的前
的前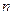 项和为
项和为 ,已知
,已知
(Ⅰ)写出
 与
与 的递推关系式
的递推关系式 ,并求
,并求 关于
关于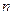 的表达式;
的表达式;(Ⅱ)设
 ,求数列
,求数列 的前
的前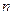 项和
项和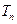 。
。22.(本大题满分14分)如图,F为双曲线C: 的右焦点。P为双曲线C右支上一点,且位于
的右焦点。P为双曲线C右支上一点,且位于 轴上方,M为左准线上一点,
轴上方,M为左准线上一点,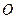 为坐标原点。已知四边形
为坐标原点。已知四边形 为平行四边形,
为平行四边形, 。
。
(Ⅰ)写出双曲线C的离心率 与
与 的关系式;
的关系式;
(Ⅱ)当 时,经过焦点F且品行于OP的直线交双曲线于A、B点,若
时,经过焦点F且品行于OP的直线交双曲线于A、B点,若 ,求此时的双曲线方程。
,求此时的双曲线方程。
 的右焦点。P为双曲线C右支上一点,且位于
的右焦点。P为双曲线C右支上一点,且位于 轴上方,M为左准线上一点,
轴上方,M为左准线上一点,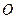 为坐标原点。已知四边形
为坐标原点。已知四边形 为平行四边形,
为平行四边形, 。
。(Ⅰ)写出双曲线C的离心率
 与
与 的关系式;
的关系式;(Ⅱ)当
 时,经过焦点F且品行于OP的直线交双曲线于A、B点,若
时,经过焦点F且品行于OP的直线交双曲线于A、B点,若 ,求此时的双曲线方程。
,求此时的双曲线方程。
 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
