全一卷
1.已知集合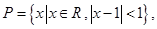
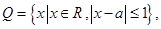 且
且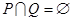 .则实数
.则实数 取值范围为.
取值范围为.
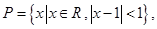
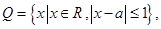 且
且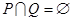 .则实数
.则实数 取值范围为.
取值范围为.A.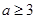 | B. | C. 或 或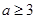 | D. |
2.若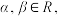 则
则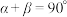 是
是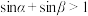 的
的
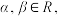 则
则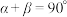 是
是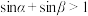 的
的| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
3.已知等比数列{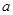
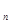 }:
}: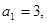 且第一项至第八项的几何平均数为9,则第三项是( )
且第一项至第八项的几何平均数为9,则第三项是( )
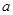
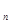 }:
}: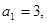 且第一项至第八项的几何平均数为9,则第三项是( )
且第一项至第八项的几何平均数为9,则第三项是( )A. | B. | C. | D. |
4.已知复数 为虚数单位),且
为虚数单位),且 ,则
,则 ()
()
 为虚数单位),且
为虚数单位),且 ,则
,则 ()
()A. | B. |
C. 或 或 | D. 或 或 |
5.已知直线 与抛物线
与抛物线 交于
交于 两点,
两点,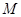 为
为 的中点,
的中点, 为抛物线上一个动点,若
为抛物线上一个动点,若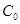 满足
满足 ,则下列一定成立的是( )。
,则下列一定成立的是( )。
 与抛物线
与抛物线 交于
交于 两点,
两点,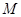 为
为 的中点,
的中点, 为抛物线上一个动点,若
为抛物线上一个动点,若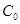 满足
满足 ,则下列一定成立的是( )。
,则下列一定成立的是( )。A. | B. 其中 其中 是抛物线过 是抛物线过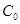 的切线 的切线 |
C. | D. |
6.某程序框图如下,当E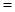 0.96时,则输出的K=( )
0.96时,则输出的K=( )
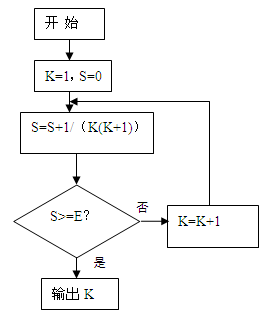
 0.96时,则输出的K=( )
0.96时,则输出的K=( )
| A.20 | B.22 | C.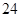 | D.25 |
7.若三位数 被7整除,且
被7整除,且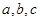 成公差非零的等差数列,则这样的整数共有( )个。
成公差非零的等差数列,则这样的整数共有( )个。
 被7整除,且
被7整除,且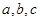 成公差非零的等差数列,则这样的整数共有( )个。
成公差非零的等差数列,则这样的整数共有( )个。| A.4 | B.6 | C.7 | D.8 |
8.设函数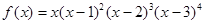 ,则函数
,则函数 的极大值点为( )
的极大值点为( )
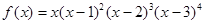 ,则函数
,则函数 的极大值点为( )
的极大值点为( )A. | B. | C.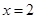 | D.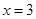 |
9.已知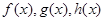 为一次函数,若对实数
为一次函数,若对实数 满足
满足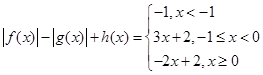 ,
,
则 的表达式为( )。
的表达式为( )。
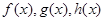 为一次函数,若对实数
为一次函数,若对实数 满足
满足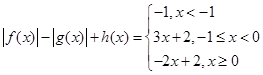 ,
,则
 的表达式为( )。
的表达式为( )。A. |
B. |
C. |
D. |
10.若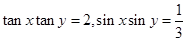 ,则
,则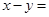
_________________ .
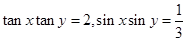 ,则
,则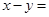
11.已知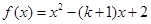 ,若当
,若当 时
时 恒大于零,则
恒大于零,则 的取值范围为
的取值范围为_____________ .
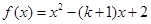 ,若当
,若当 时
时 恒大于零,则
恒大于零,则 的取值范围为
的取值范围为12.数列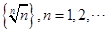 ,则数列中最大项的值为
,则数列中最大项的值为______________ .
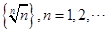 ,则数列中最大项的值为
,则数列中最大项的值为13.若 ,满足
,满足 ,则
,则 ,
, 。
。
 ,满足
,满足 ,则
,则 ,
, 。
。14.设直线 与曲线
与曲线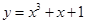 有三个不同的交点
有三个不同的交点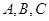 ,且
,且 ,则直线
,则直线 的方程为
的方程为_________________ .
 与曲线
与曲线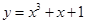 有三个不同的交点
有三个不同的交点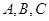 ,且
,且 ,则直线
,则直线 的方程为
的方程为15.若 则
则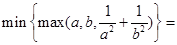
________________________ .
 则
则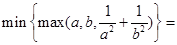
16.某动点在平 面直角坐标系 第一 象限的整点上运动 (含第一象限x轴、y轴上的整点),其运动规律为 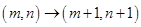 或
或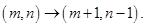 若该动点从原点出发,经过 6步运动到点
若该动点从原点出发,经过 6步运动到点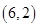 ,则有
,则有_______ 中不同的运动轨迹.
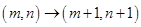 或
或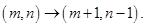 若该动点从原点出发,经过 6步运动到点
若该动点从原点出发,经过 6步运动到点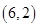 ,则有
,则有17.已知抛物线 ,过
,过 轴上一点
轴上一点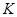 的直线与抛物线交于点
的直线与抛物线交于点 两点。
两点。
证明,存在唯一一点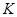 ,使得
,使得 为常数,并确定
为常数,并确定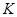 点的坐标。
点的坐标。
 ,过
,过 轴上一点
轴上一点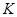 的直线与抛物线交于点
的直线与抛物线交于点 两点。
两点。证明,存在唯一一点
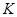 ,使得
,使得 为常数,并确定
为常数,并确定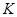 点的坐标。
点的坐标。18.设二次函数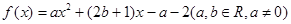 在[3,4]上至少有一个零点,求
在[3,4]上至少有一个零点,求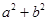 的最小值。
的最小值。
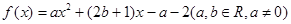 在[3,4]上至少有一个零点,求
在[3,4]上至少有一个零点,求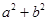 的最小值。
的最小值。19.设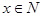 满足
满足 数列
数列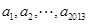 是公差为
是公差为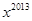 ,首项
,首项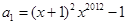 的等差数列; 数列
的等差数列; 数列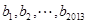 是公比为
是公比为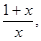 首项
首项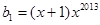 的等比数列,求证:
的等比数列,求证: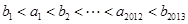 。
。
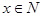 满足
满足 数列
数列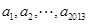 是公差为
是公差为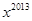 ,首项
,首项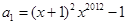 的等差数列; 数列
的等差数列; 数列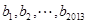 是公比为
是公比为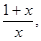 首项
首项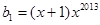 的等比数列,求证:
的等比数列,求证: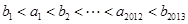 。
。20.设 证明
证明
 。
。
 证明
证明 。
。21.从0,1,2,,10中挑选若干个不同的数字填满图中每一个圆圈称为一种“填法”,若各条线段相连的两个圆圈内的数字之差的绝对值各不相同,则称这样的填法为“完美填法”.
试问:对图1和图2是否存在完美填法?若存在,请给出一种完美填法;若不存在,请说明理由.

试问:对图1和图2是否存在完美填法?若存在,请给出一种完美填法;若不存在,请说明理由.


 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
