全一卷
1.设集合 ,
, ,则
,则 ( )
( )
 ,
, ,则
,则 ( )
( )A. | B. | C. | D. |
2.定义域为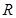 的四个函数
的四个函数 ,
, ,
, ,
, 中,奇函数的个数是
中,奇函数的个数是
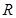 的四个函数
的四个函数 ,
, ,
, ,
, 中,奇函数的个数是
中,奇函数的个数是A.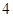 | B. | C. | D.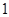 |
3.若复数 满足
满足 ,则在复平面内,
,则在复平面内, 对应的点的坐标是
对应的点的坐标是
 满足
满足 ,则在复平面内,
,则在复平面内, 对应的点的坐标是
对应的点的坐标是A. | B. | C. | D. |
4.已知离散型随机变量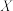 的分布列为
的分布列为
则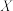 的数学期望
的数学期望
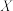 的分布列为
的分布列为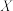 |  |  | 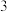 |
 |  |  |  |
则
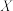 的数学期望
的数学期望
A. | B. | C.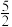 | D.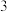 |
5.某四棱台的三视图如图所示,则该四棱台的体积是()


| A.4 | B. | C. | D.6 |
6.设 ,
, 是两条不同的直线,
是两条不同的直线, ,
, 是两个不同的平面,下列命题中正确的是
是两个不同的平面,下列命题中正确的是
 ,
, 是两条不同的直线,
是两条不同的直线, ,
, 是两个不同的平面,下列命题中正确的是
是两个不同的平面,下列命题中正确的是A.若 , , , , ,则 ,则 |
B.若 , , , , ,则 ,则 |
C.若 , , , , ,则 ,则 |
D.若 , , , , ,则 ,则 |
7.已知中心在原点的双曲线 的右焦点为
的右焦点为 ,离心率等于
,离心率等于 ,在双曲线
,在双曲线 的方程是
的方程是
 的右焦点为
的右焦点为 ,离心率等于
,离心率等于 ,在双曲线
,在双曲线 的方程是
的方程是 A. | B. | C. | D. |
8.设整数 ,集合
,集合 .令集合
.令集合 若
若 和
和 都在
都在 中,则下列选项正确的是( )
中,则下列选项正确的是( )
 ,集合
,集合 .令集合
.令集合 若
若 和
和 都在
都在 中,则下列选项正确的是( )
中,则下列选项正确的是( )A. , , | B. , , |
C. , , | D. , , |
9.不等式 的解集为
的解集为___________ .
 的解集为
的解集为10.若曲线 在点
在点 处的切线平行于
处的切线平行于 轴,则
轴,则 .
.
 在点
在点 处的切线平行于
处的切线平行于 轴,则
轴,则 .
.11.执行如图所示的程序框图,若输入 的值为
的值为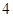 ,则输出
,则输出 的值为______.
的值为______.
 的值为
的值为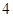 ,则输出
,则输出 的值为______.
的值为______.
12.在等差数列 中,已知
中,已知 ,则
,则

_____ .
 中,已知
中,已知 ,则
,则

13.给定区域 :,令点集
:,令点集 是
是 在
在 上取得最大值或最小值的点
上取得最大值或最小值的点 ,则
,则 中的点共确定
中的点共确定______ 条不同的直线.
 :,令点集
:,令点集 是
是 在
在 上取得最大值或最小值的点
上取得最大值或最小值的点 ,则
,则 中的点共确定
中的点共确定14.已知曲线 的参数方程为
的参数方程为 (
( 为参数),
为参数), 在点
在点 处的切线为
处的切线为 ,以坐标原点为极点,
,以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,则
轴的正半轴为极轴建立极坐标系,则 的极坐标方程为_____________.
的极坐标方程为_____________.
 的参数方程为
的参数方程为 (
( 为参数),
为参数), 在点
在点 处的切线为
处的切线为 ,以坐标原点为极点,
,以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,则
轴的正半轴为极轴建立极坐标系,则 的极坐标方程为_____________.
的极坐标方程为_____________.15.如图, 是圆
是圆 的直径,点
的直径,点 在圆
在圆 上,延长
上,延长 到
到 使
使 ,过
,过 作圆
作圆 的切线交
的切线交 于
于 .若
.若 ,
, ,则
,则
_________ .

 是圆
是圆 的直径,点
的直径,点 在圆
在圆 上,延长
上,延长 到
到 使
使 ,过
,过 作圆
作圆 的切线交
的切线交 于
于 .若
.若 ,
, ,则
,则

16.已知函数 ,
, .
.
(Ⅰ) 求 的值;
的值;
(Ⅱ) 若 ,
, ,求
,求 .
.
 ,
, .
.(Ⅰ) 求
 的值;
的值; (Ⅱ) 若
 ,
, ,求
,求 .
.17.某车间共有 名工人,随机抽取
名工人,随机抽取 名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.

(Ⅰ) 根据茎叶图计算样本均值;
(Ⅱ) 日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间 名工人中有几名优秀工人;
名工人中有几名优秀工人;
(Ⅲ) 从该车间 名工人中,任取
名工人中,任取 人,求恰有
人,求恰有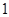 名优秀工人的概率.
名优秀工人的概率.
 名工人,随机抽取
名工人,随机抽取 名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
(Ⅰ) 根据茎叶图计算样本均值;
(Ⅱ) 日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间
 名工人中有几名优秀工人;
名工人中有几名优秀工人;(Ⅲ) 从该车间
 名工人中,任取
名工人中,任取 人,求恰有
人,求恰有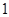 名优秀工人的概率.
名优秀工人的概率.18.如图1,在等腰直角三角形 中,
中,  ,
,  ,
, 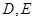 分别是
分别是 上的点,
上的点,  ,
,
 为
为 的中点.将
的中点.将 沿
沿 折起,得到如图2所示的四棱锥
折起,得到如图2所示的四棱锥 ,其中
,其中 .
.

(Ⅰ) 证明: 平面
平面 ;
;
(Ⅱ) 求二面角 的平面角的余弦值.
的平面角的余弦值.
 中,
中,  ,
,  ,
, 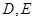 分别是
分别是 上的点,
上的点,  ,
, 为
为 的中点.将
的中点.将 沿
沿 折起,得到如图2所示的四棱锥
折起,得到如图2所示的四棱锥 ,其中
,其中 .
.
(Ⅰ) 证明:
 平面
平面 ;
;(Ⅱ) 求二面角
 的平面角的余弦值.
的平面角的余弦值.19.设数列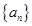 的前
的前 项和为
项和为 .已知
.已知 ,
, ,
, .
.
(Ⅰ) 求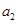 的值;
的值;
(Ⅱ) 求数列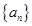 的通项公式;
的通项公式;
(Ⅲ) 证明:对一切正整数 ,有
,有 .
.
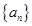 的前
的前 项和为
项和为 .已知
.已知 ,
, ,
, .
.(Ⅰ) 求
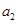 的值;
的值;(Ⅱ) 求数列
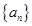 的通项公式;
的通项公式;(Ⅲ) 证明:对一切正整数
 ,有
,有 .
.20.已知抛物线 的顶点为原点,其焦点
的顶点为原点,其焦点 到直线
到直线 的距离为
的距离为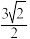 .设
.设 为直线
为直线 上的点,过点
上的点,过点 作抛物线
作抛物线 的两条切线
的两条切线 ,其中
,其中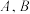 为切点.
为切点.
(1) 求抛物线 的方程;
的方程;
(2) 当点 为直线
为直线 上的定点时,求直线
上的定点时,求直线 的方程;
的方程;
(3) 当点 在直线
在直线 上移动时,求
上移动时,求 的最小值.
的最小值.
 的顶点为原点,其焦点
的顶点为原点,其焦点 到直线
到直线 的距离为
的距离为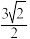 .设
.设 为直线
为直线 上的点,过点
上的点,过点 作抛物线
作抛物线 的两条切线
的两条切线 ,其中
,其中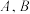 为切点.
为切点.(1) 求抛物线
 的方程;
的方程;(2) 当点
 为直线
为直线 上的定点时,求直线
上的定点时,求直线 的方程;
的方程;(3) 当点
 在直线
在直线 上移动时,求
上移动时,求 的最小值.
的最小值.21.设函数 (其中
(其中 ).
).
(Ⅰ)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ)当 时,求函数
时,求函数 在
在 上的最大值
上的最大值 .
.
 (其中
(其中 ).
).(Ⅰ)当
 时,求函数
时,求函数 的单调区间;
的单调区间;(Ⅱ)当
 时,求函数
时,求函数 在
在 上的最大值
上的最大值 .
. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
