全一卷
1.已知如下数组
① ②
②
③ ④
④ .
.
其中可作为直角三角形三边长度的数组是( ).
①
 ②
②
③
 ④
④ .
.其中可作为直角三角形三边长度的数组是( ).
| A.①,④ | B.②,④ | C.②,③ | D.③,④ |
2.在下面时间段内,时钟的时针与分针会出现重合的是( )
| A.5:25~5:26 | B.5:26~5:27 |
| C.5:27~5:28 | D.5:28~5:29 |
3.已知 ,使
,使 为正数的自然数有.
为正数的自然数有.
 ,使
,使 为正数的自然数有.
为正数的自然数有.| A.1个 | B.2个 | C.多于2的有限个 | D.无限多个 |
4.将长度为20的铁丝围成三边长均为整数的三角形,那么,不全等的三角形的个数是( ).
| A.5 | B.6 | C.8 | D.10 |
5.在 中,
中, ,
, ,
, .则
.则 的面积等于( ).
的面积等于( ).
 中,
中, ,
, ,
, .则
.则 的面积等于( ).
的面积等于( ).| A.16 | B.18 | C. | D. |
6.已知 ,
, ,
, ,
, ,
, .则
.则 、
、 、
、 、
、 、
、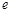 的大小关系是( ).
的大小关系是( ).
 ,
, ,
, ,
, ,
, .则
.则 、
、 、
、 、
、 、
、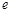 的大小关系是( ).
的大小关系是( ).A. | B. | C. | D. |
7.化简 ________.
________.
 ________.
________.8.如图, 为正方形
为正方形 内一点,
内一点, ,并且
,并且 点到
点到 边的距离也等于10.那么,正方形
边的距离也等于10.那么,正方形 的面积是________.
的面积是________.
 为正方形
为正方形 内一点,
内一点, ,并且
,并且 点到
点到 边的距离也等于10.那么,正方形
边的距离也等于10.那么,正方形 的面积是________.
的面积是________.
9.已知 为整数,
为整数, 是质数.那么,
是质数.那么, 的所有可能值的和为__________.
的所有可能值的和为__________.
 为整数,
为整数, 是质数.那么,
是质数.那么, 的所有可能值的和为__________.
的所有可能值的和为__________.10.如图, 为平行四边形
为平行四边形 内一点,过点
内一点,过点 分别作
分别作 、
、 的平行线交平行四边形于
的平行线交平行四边形于 、
、 、
、 、
、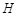 四点.若
四点.若 ,
, ,则
,则 __________.
__________.
 为平行四边形
为平行四边形 内一点,过点
内一点,过点 分别作
分别作 、
、 的平行线交平行四边形于
的平行线交平行四边形于 、
、 、
、 、
、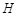 四点.若
四点.若 ,
, ,则
,则 __________.
__________.
11.实数 、
、 、
、 、
、 满足
满足 ,
, .则
.则 之值是__________.
之值是__________.
 、
、 、
、 、
、 满足
满足 ,
, .则
.则 之值是__________.
之值是__________.12.多项式 的一个因式是
的一个因式是 .则
.则 的值为__________.
的值为__________.
 的一个因式是
的一个因式是 .则
.则 的值为__________.
的值为__________.13.梯形的两条对角线互相垂直,其中一条对角线的长是5厘米,梯形的高等于4厘米.那么,梯形的面积是__________.
14.某商场有一部自动扶梯匀速由下而上运动,甲、乙二人都急于上楼办事,因此在乘扶梯的同时匀速登梯,甲登了55级后到达楼上,乙登梯速度是甲的2倍(单位时间乙登楼梯级数是甲的2倍),他登了60级后到达楼上.那么,由楼下到楼上自动扶梯级数为__________.
15.若 ,
, .则
.则 __________.
__________.
 ,
, .则
.则 __________.
__________.16.如图,等腰直角三角形 中,
中, 为斜边
为斜边 的中点,
的中点, 、
、 分别为腰
分别为腰 、
、 上(异于端点)的点,
上(异于端点)的点, ,
,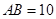 .设
.设 ,则
,则 的取值范围是__________.
的取值范围是__________.
 中,
中, 为斜边
为斜边 的中点,
的中点, 、
、 分别为腰
分别为腰 、
、 上(异于端点)的点,
上(异于端点)的点, ,
,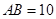 .设
.设 ,则
,则 的取值范围是__________.
的取值范围是__________.
17.实数 、
、 满足
满足 .则
.则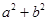 的最大值为__________.
的最大值为__________.
 、
、 满足
满足 .则
.则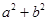 的最大值为__________.
的最大值为__________.18.若 、
、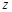 均为质数,
均为质数, ,且
,且 、
、 、
、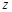 .满足
.满足 .则
.则 __________.
__________.
 、
、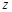 均为质数,
均为质数, ,且
,且 、
、 、
、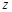 .满足
.满足 .则
.则 __________.
__________.19.黑板上写有1,2,3,…,1997,1998这1998个自然数,对它们进行操作。每次操作规则如下:擦掉写在黑板上的三个数后,再添写上所擦掉三个数之和的个位数子,例如:擦掉5,13和1998后,添加上6;若再擦掉6,6,38,添加上0,等等,如果经过998次操作后,发现黑板上剩下两个数,一个是25,则另一个是__________.
20.今有浓度为5%、8%、9%的甲、乙、丙三种盐水分别为60克、60克、47克.现要配制浓度为7%的盐水100克,问甲种盐水最多可用多少克?最少可用多少克?
21.矩形 中,
中,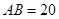 厘米,
厘米, 厘米,若在
厘米,若在 、
、 上各取一点
上各取一点 、
、 (如图).使
(如图).使 的值最小,求这个最小值.
的值最小,求这个最小值.
 中,
中,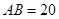 厘米,
厘米, 厘米,若在
厘米,若在 、
、 上各取一点
上各取一点 、
、 (如图).使
(如图).使 的值最小,求这个最小值.
的值最小,求这个最小值.
22.国际象棋比赛中.胜局一得1分,平一局得0.5分,负一局得0分。今有8名选手进行单循环比赛(每两人均赛一局),赛完后、发现各选手的得分均不相同,当按得分由大到小排列好名次后,第四名选手得4.5分,第二名的得分等于最后四名选手得分总和.问前三名选手各得多少分?说明理由.
23.如图,正方形 被两条与边平行的线段
被两条与边平行的线段 分割成4个小矩形,
分割成4个小矩形, 是
是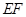 与
与 的交点,若矩形
的交点,若矩形 的面积恰好是矩形
的面积恰好是矩形 面积的两倍,试确定
面积的两倍,试确定 的大小,并证明你的结论.
的大小,并证明你的结论.
 被两条与边平行的线段
被两条与边平行的线段 分割成4个小矩形,
分割成4个小矩形, 是
是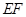 与
与 的交点,若矩形
的交点,若矩形 的面积恰好是矩形
的面积恰好是矩形 面积的两倍,试确定
面积的两倍,试确定 的大小,并证明你的结论.
的大小,并证明你的结论.
24.化简 的结果是( ).
的结果是( ).
 的结果是( ).
的结果是( ).A. | B. | C. | D. |
25. ,
, 那么,
那么, 与
与 的关系是( ).
的关系是( ).
 ,
, 那么,
那么, 与
与 的关系是( ).
的关系是( ).A. | B. | C. | D. |
26. 的内切圆切斜边
的内切圆切斜边 于点
于点 ,
, ,
, .则内切圆的半径等于( ).
.则内切圆的半径等于( ).
 的内切圆切斜边
的内切圆切斜边 于点
于点 ,
, ,
, .则内切圆的半径等于( ).
.则内切圆的半径等于( ).| A.6 | B. | C. | D.2 |
27.函数 的值域是集合
的值域是集合 .则
.则 中不属于
中不属于 的元素是( ).
的元素是( ).
 的值域是集合
的值域是集合 .则
.则 中不属于
中不属于 的元素是( ).
的元素是( ).| A.2 | B.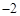 | C.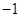 | D. |
28.已知函数 的图象过点
的图象过点 ,那么函数
,那么函数 的图象过点( ).
的图象过点( ).
 的图象过点
的图象过点 ,那么函数
,那么函数 的图象过点( ).
的图象过点( ).A. | B. | C. | D. |
29.我们规定真命题赋值为1,假命题赋值为0.“1”或“0”均称作命题的“真值”
命题 :“在同一个直角坐标系中,曲线
:“在同一个直角坐标系中,曲线 的图象与
的图象与 的图象至多有一个交点.”那么,命题
的图象至多有一个交点.”那么,命题 的真值是__________.
的真值是__________.
命题
 :“在同一个直角坐标系中,曲线
:“在同一个直角坐标系中,曲线 的图象与
的图象与 的图象至多有一个交点.”那么,命题
的图象至多有一个交点.”那么,命题 的真值是__________.
的真值是__________.30.在正方体 中,过
中,过 、
、 、
、 三点的平面记为
三点的平面记为 ,过
,过 、
、 、
、 三点的平面记为
三点的平面记为 .那么,
.那么, 为__________.
为__________.
 中,过
中,过 、
、 、
、 三点的平面记为
三点的平面记为 ,过
,过 、
、 、
、 三点的平面记为
三点的平面记为 .那么,
.那么, 为__________.
为__________.31.已知 .则
.则 的值为__________.
的值为__________.
 .则
.则 的值为__________.
的值为__________.32.已知存在整数 、
、 、
、 使等式
使等式 对任意实数
对任意实数 都成立.则
都成立.则 的值为__________.
的值为__________.
 、
、 、
、 使等式
使等式 对任意实数
对任意实数 都成立.则
都成立.则 的值为__________.
的值为__________.33.实数 、
、 、
、 、
、 满足
满足 及
及 .那么
.那么 的最小值为__________.
的最小值为__________.
 、
、 、
、 、
、 满足
满足 及
及 .那么
.那么 的最小值为__________.
的最小值为__________.34.方程 的解集为__________.
的解集为__________.
 的解集为__________.
的解集为__________.35.若 且
且 ,那么,
,那么, 的值为__________.
的值为__________.
 且
且 ,那么,
,那么, 的值为__________.
的值为__________.36.如图所示,三棱柱 中,全部的九条棱长都等于1,且
中,全部的九条棱长都等于1,且 ,P为侧面
,P为侧面 的对角线A1B上一点,
的对角线A1B上一点, ,连
,连 .异面直线
.异面直线 与AC所成角的度数为
与AC所成角的度数为__________ .
 中,全部的九条棱长都等于1,且
中,全部的九条棱长都等于1,且 ,P为侧面
,P为侧面 的对角线A1B上一点,
的对角线A1B上一点, ,连
,连 .异面直线
.异面直线 与AC所成角的度数为
与AC所成角的度数为
37.设函数 对任意实数
对任意实数 都有
都有 .则
.则 __________.
__________.
 对任意实数
对任意实数 都有
都有 .则
.则 __________.
__________.38. 的内切圆分别切
的内切圆分别切 、
、 、
、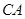 三边于
三边于 、
、 、
、 ,
, 的内切圆分别切三边
的内切圆分别切三边 、
、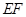 、
、 于
于 、
、 、
、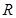 .已知
.已知 ∽
∽ ,
, 的周长等于3.则
的周长等于3.则 的面积等于__________.
的面积等于__________.
 的内切圆分别切
的内切圆分别切 、
、 、
、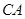 三边于
三边于 、
、 、
、 ,
, 的内切圆分别切三边
的内切圆分别切三边 、
、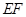 、
、 于
于 、
、 、
、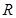 .已知
.已知 ∽
∽ ,
, 的周长等于3.则
的周长等于3.则 的面积等于__________.
的面积等于__________.39.已知 ,
, ,
, 都是定义在
都是定义在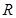 上的函数.我们定义上的函数为
上的函数.我们定义上的函数为 、
、 、
、 、
、 的最小值.则
的最小值.则 的最大值等于__________.
的最大值等于__________.
 ,
, ,
, 都是定义在
都是定义在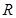 上的函数.我们定义上的函数为
上的函数.我们定义上的函数为 、
、 、
、 、
、 的最小值.则
的最小值.则 的最大值等于__________.
的最大值等于__________.40.已知 .则
.则 __________.
__________.
 .则
.则 __________.
__________.41.长方体 中,
中, ,
, ,
, .过
.过 作长方体的截面,则所得截面多边形面积的最小值是__________.
作长方体的截面,则所得截面多边形面积的最小值是__________.
 中,
中, ,
, ,
, .过
.过 作长方体的截面,则所得截面多边形面积的最小值是__________.
作长方体的截面,则所得截面多边形面积的最小值是__________.42. 是定义在
是定义在 上且取值为整数的严格增函数(如果任意
上且取值为整数的严格增函数(如果任意 、
、 ,当
,当 时,有
时,有 ,则称
,则称 是
是 上的严格增函数),当
上的严格增函数),当 、
、 互质时,有
互质时,有 .若
.若 ,试求
,试求 的值.
的值.
 是定义在
是定义在 上且取值为整数的严格增函数(如果任意
上且取值为整数的严格增函数(如果任意 、
、 ,当
,当 时,有
时,有 ,则称
,则称 是
是 上的严格增函数),当
上的严格增函数),当 、
、 互质时,有
互质时,有 .若
.若 ,试求
,试求 的值.
的值.43.如图,在四棱锥 中,底面正方形
中,底面正方形 的边长为
的边长为 ,侧棱
,侧棱 ,
, 为棱
为棱 的中点,
的中点, 为棱
为棱 的中点.求异面直线
的中点.求异面直线 与
与 所成角的余弦值.
所成角的余弦值.
 中,底面正方形
中,底面正方形 的边长为
的边长为 ,侧棱
,侧棱 ,
, 为棱
为棱 的中点,
的中点, 为棱
为棱 的中点.求异面直线
的中点.求异面直线 与
与 所成角的余弦值.
所成角的余弦值.
44.若 ,求证:对任意的实数
,求证:对任意的实数 ,关于
,关于 的方程
的方程 都有两个不等的实数根.
都有两个不等的实数根.
 ,求证:对任意的实数
,求证:对任意的实数 ,关于
,关于 的方程
的方程 都有两个不等的实数根.
都有两个不等的实数根.45.有1998名运动员号码为1~1998这1998个自然数,从中选出若干名运动员参加仪仗队,但要使剩下的运动员中没有一个人的号码数等于另外两人的号码数的乘积.那么,选为仪仗队的运动员至少能有多少人?给出你的选取方案,并简述理由.
 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
