全一卷
1.若 ,
, ,且
,且 ,则
,则 的值( ).
的值( ).
 ,
, ,且
,且 ,则
,则 的值( ).
的值( ).A.等于 | B.等于1 | C.等于0 | D.不是与 、 、 无关的常数 无关的常数 |
2.若非空集合 ,
, ,则能使
,则能使 成立的所有
成立的所有 的集合是.
的集合是.
 ,
, ,则能使
,则能使 成立的所有
成立的所有 的集合是.
的集合是.A. | B. | C. | D. |
3.各项均为实数的等比数列{an}前n项之和记为 ,若
,若 ,
, , 则
, 则 等于
等于
 ,若
,若 ,
, , 则
, 则 等于
等于| A.150 | B.-200 | C.150或-200 | D.-50或400 |
4.设命题 :关于
:关于 的不等式
的不等式 与
与 的解集相同;命题
的解集相同;命题 :
: .则命题
.则命题 ( ).
( ).
 :关于
:关于 的不等式
的不等式 与
与 的解集相同;命题
的解集相同;命题 :
: .则命题
.则命题 ( ).
( ).A.是命题 的充分必要条件 的充分必要条件 | B.是命题 的充分条件但不是必要条件 的充分条件但不是必要条件 |
C.是命题 的必要条件但不是充分条件 的必要条件但不是充分条件 | D.既不是命题 的充分条件也不是命题 的充分条件也不是命题 的必要条件 的必要条件 |
5.设 、
、 、
、 分别是正四面体
分别是正四面体 的棱
的棱 、
、 、
、 的中点.则二面角
的中点.则二面角 的大小是( ).
的大小是( ).

 、
、 、
、 分别是正四面体
分别是正四面体 的棱
的棱 、
、 、
、 的中点.则二面角
的中点.则二面角 的大小是( ).
的大小是( ).
A. | B. | C. | D. |
6.在正方体的8个顶点、12条棱的中点、6个面的中心及正方体的中心共27个点中,共线的三点组的个数是( ).
| A.57 | B.49 | C.43 | D.37 |
7.若 是以2为周期的偶函数,当
是以2为周期的偶函数,当 时,
时, ,则
,则 ,
, ,
, 由小到大的排列是______.
由小到大的排列是______.
 是以2为周期的偶函数,当
是以2为周期的偶函数,当 时,
时, ,则
,则 ,
, ,
, 由小到大的排列是______.
由小到大的排列是______.8.设复数 ,复数
,复数 、
、 、
、 在复平面上对应的三个点分别是
在复平面上对应的三个点分别是 、
、 、
、 .当
.当 、
、 、
、 不共线时,以线段
不共线时,以线段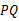 、
、 为两边的平行四边形的第四个顶点为
为两边的平行四边形的第四个顶点为 .则点
.则点 到原点距离的最大值是______.
到原点距离的最大值是______.
 ,复数
,复数 、
、 、
、 在复平面上对应的三个点分别是
在复平面上对应的三个点分别是 、
、 、
、 .当
.当 、
、 、
、 不共线时,以线段
不共线时,以线段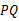 、
、 为两边的平行四边形的第四个顶点为
为两边的平行四边形的第四个顶点为 .则点
.则点 到原点距离的最大值是______.
到原点距离的最大值是______.9.从0,1,2,3,4,5,6,7,8,9这10个数中取出3个数,使其和为不小于10的偶数,不同的取法有______ .
10.各项为实数的等差数列的公差为4,其首项的平方与其余各项之和不超过100.这样的数列至多有______ 项.
11.已知椭圆 与抛物线
与抛物线 有公共点.则a的取值范围是
有公共点.则a的取值范围是_______ .
 与抛物线
与抛物线 有公共点.则a的取值范围是
有公共点.则a的取值范围是12. 中,
中, ,
, ,
, ,
, 是
是 的中点.将
的中点.将 沿
沿 折起,使
折起,使 、
、 两点间的距离为
两点间的距离为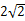 ,此时三棱锥
,此时三棱锥 的体积等于______.
的体积等于______.
 中,
中, ,
, ,
, ,
, 是
是 的中点.将
的中点.将 沿
沿 折起,使
折起,使 、
、 两点间的距离为
两点间的距离为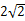 ,此时三棱锥
,此时三棱锥 的体积等于______.
的体积等于______.
13.已知复数 .求
.求 的共轭复数
的共轭复数 的幅角主值.
的幅角主值.
 .求
.求 的共轭复数
的共轭复数 的幅角主值.
的幅角主值.14.设函数 .对于给定的负数
.对于给定的负数 ,有一个最大的正数
,有一个最大的正数 ,使得在整个区间
,使得在整个区间 上,不等式
上,不等式 都成立.问:
都成立.问: 为何值时
为何值时 最大?求出这个最大的
最大?求出这个最大的 .证明你的结论.
.证明你的结论.
 .对于给定的负数
.对于给定的负数 ,有一个最大的正数
,有一个最大的正数 ,使得在整个区间
,使得在整个区间 上,不等式
上,不等式 都成立.问:
都成立.问: 为何值时
为何值时 最大?求出这个最大的
最大?求出这个最大的 .证明你的结论.
.证明你的结论.15.已知抛物线 及定点
及定点 、
、 .
. 是抛物线上的点,设直线
是抛物线上的点,设直线 、
、 与抛物线的另一交点分别为
与抛物线的另一交点分别为 、
、 .求证:当点
.求证:当点 在抛物线上变动时(只要
在抛物线上变动时(只要 、
、 存在且
存在且 ),直线
),直线 恒过一个定点,并求出这个定点的坐标.
恒过一个定点,并求出这个定点的坐标.
 及定点
及定点 、
、 .
. 是抛物线上的点,设直线
是抛物线上的点,设直线 、
、 与抛物线的另一交点分别为
与抛物线的另一交点分别为 、
、 .求证:当点
.求证:当点 在抛物线上变动时(只要
在抛物线上变动时(只要 、
、 存在且
存在且 ),直线
),直线 恒过一个定点,并求出这个定点的坐标.
恒过一个定点,并求出这个定点的坐标.16.如图, 、
、 分别为
分别为 的外心和内心,
的外心和内心, 是
是 边上的高,
边上的高, 在线段
在线段 上.求证:
上.求证: 的外接圆半径等于
的外接圆半径等于 边上的旁切圆半径.注:
边上的旁切圆半径.注: 的
的 边上的旁切圆是与边
边上的旁切圆是与边 、
、 的延长线以及边
的延长线以及边 都相切的圆.
都相切的圆.

 、
、 分别为
分别为 的外心和内心,
的外心和内心, 是
是 边上的高,
边上的高, 在线段
在线段 上.求证:
上.求证: 的外接圆半径等于
的外接圆半径等于 边上的旁切圆半径.注:
边上的旁切圆半径.注: 的
的 边上的旁切圆是与边
边上的旁切圆是与边 、
、 的延长线以及边
的延长线以及边 都相切的圆.
都相切的圆.
17.设 且
且 .求证:
.求证: .并问:等号成立的充要条件.
.并问:等号成立的充要条件.
 且
且 .求证:
.求证: .并问:等号成立的充要条件.
.并问:等号成立的充要条件.18.对于正整数 、
、 ,定义
,定义 ,其中
,其中 、
、 为非负整数,
为非负整数, ,且
,且 .求最大的正整数
.求最大的正整数 ,使得存在正整数
,使得存在正整数 ,对于任意的正整数
,对于任意的正整数 ,都有
,都有 .证明你的结论.
.证明你的结论.
 、
、 ,定义
,定义 ,其中
,其中 、
、 为非负整数,
为非负整数, ,且
,且 .求最大的正整数
.求最大的正整数 ,使得存在正整数
,使得存在正整数 ,对于任意的正整数
,对于任意的正整数 ,都有
,都有 .证明你的结论.
.证明你的结论. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
