搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．已知i是虚数单位，则（﹣1+i）（2﹣i）=（ ）
| A．﹣3+i | B．﹣1+3i | C．﹣3+3i | D．﹣1+i |
2．设集合S={x|x＞﹣2}，T={x|x2+3x﹣4≤0}，则（∁RS）∪T=（ ）
| A．（﹣2，1] | B．（﹣∞，﹣4] | C．（﹣∞，1] | D．[1，+∞） |
3．已知x，y为正实数，则（ ）
| A．2lgx+lgy=2lgx+2lgy | B．2lg（x+y）=2lgx•2lgy |
| C．2lgx•lgy=2lgx+2lgy | D．2lg（xy）=2lgx•2lgy |
4． f（x）=Acos（ωx+φ）（A＞0，ω＞0，φ∈R），则“f（x）是奇函数”是“φ=
”的（ ）
”的（ ）| A．充分不必要条件 | B．必要不充分条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
5．某程序框图如图所示，若该程序运行后输出的值是
，则（ ）
，则（ ）
| A．a=4 | B．a=5 | C．a=6 | D．a=7 |
6．（2013•浙江）已知
，则tan2α=（）
，则tan2α=（）A． | B． | C． | D． |
7．（2013•浙江）设△ABC，P0是边AB上一定点，满足
，且对于边AB上任一点P，恒有
则（）
，且对于边AB上任一点P，恒有
则（）| A．∠ABC=90° | B．∠BAC=90° | C．AB=AC | D．AC=BC |
8．已知e为自然对数的底数,设函数
,则．
,则．| A．当k=1时,f(x)在x=1处取到极小值 | B．当k=1时,f(x)在x=1处取到极大值 |
| C．当k=2时,f(x)在x=1处取到极小值 | D．当k=2时,f(x)在x=1处取到极大值 |
9．（2013•浙江）如图F1、F2是椭圆C1：
+y2=1与双曲线C2的公共焦点A、B分别是C1、C2在第二、四象限的公共点，若四边形AF1BF2为矩形，则C2的离心率是（ ）
A．
B．
C．
D．
+y2=1与双曲线C2的公共焦点A、B分别是C1、C2在第二、四象限的公共点，若四边形AF1BF2为矩形，则C2的离心率是（ ）
A．
B．
C．
D．
10．在空间中，过点A作平面π的垂线，垂足为B，记B=fπ（A）．设α，β是两个不同的平面，对空间任意一点P，Q1=fβ[fα（P）]，Q2=fα[fβ（P）]，恒有PQ1=PQ2，则（ ）
| A．平面α与平面β垂直 |
| B．平面α与平面β所成的（锐）二面角为45° |
| C．平面α与平面β平行 |
| D．平面α与平面β所成的（锐）二面角为60° |
11．设二项式
的展开式中常数项为A，则A=___________ ．
的展开式中常数项为A，则A=12．若某几何体的三视图（单位：cm）如图所示，则此几何体的体积等于 _________ cm3．
13．设z=kx+y,其中实数x、y满足
若z的最大值为12,则实数k=___________ ．
若z的最大值为12,则实数k=14．将A，B，C，D，E，F六个字母排成一排，且A，B均在C的同侧，则不同的排法共有___________ 种（用数字作答）
15．设F为抛物线C：y2=4x的焦点，过点P（﹣1，0）的直线l交抛物线C于两点A，B，点Q为线段AB的中点，若|FQ|=2，则直线l的斜率等于 _________ ．
16．△ABC中,∠C=90°,M是BC的中点,若
,则sin∠BAC=___________ ．
,则sin∠BAC=17．设
、
为单位向量，非零向量
=x+y，x、y∈R．若、的夹角为30°，则
的最大值等于___________ ．
、
为单位向量，非零向量
=x+y，x、y∈R．若、的夹角为30°，则
的最大值等于18．在公差为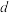
的等差数列
中,已知
，且
成等比数列.
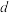的等差数列
中,已知
，且
成等比数列.（Ⅰ）求
；
（Ⅱ）若
,求
.
19．设袋子中装有a个红球，b个黄球，c个蓝球，且规定：取出一个红球得1分，取出一个黄球2分，取出蓝球得3分．
（1）当a=3，b=2，c=1时，从该袋子中任取（有放回，且每球取到的机会均等）2个球，记随机变量ξ为取出此2球所得分数之和．，求ξ分布列；
（2）从该袋子中任取（且每球取到的机会均等）1个球，记随机变量η为取出此球所得分数．若
，求a：b：c．
（1）当a=3，b=2，c=1时，从该袋子中任取（有放回，且每球取到的机会均等）2个球，记随机变量ξ为取出此2球所得分数之和．，求ξ分布列；
（2）从该袋子中任取（且每球取到的机会均等）1个球，记随机变量η为取出此球所得分数．若
，求a：b：c．20．如图，在四面体A﹣BCD中，AD⊥平面BCD，BC⊥CD，AD=2，BD=2
．M是AD的中点，P是BM的中点，点Q在线段AC上，且AQ=3QC．
（1）证明：PQ∥平面BCD；
（2）若二面角C﹣BM﹣D的大小为60°，求∠BDC的大小．
．M是AD的中点，P是BM的中点，点Q在线段AC上，且AQ=3QC．（1）证明：PQ∥平面BCD；
（2）若二面角C﹣BM﹣D的大小为60°，求∠BDC的大小．
21．图，点P（0，﹣1）是椭圆C1：
+
=1（a＞b＞0）的一个顶点，C1的长轴是圆C2：x2+y2=4的直径，l1，l2是过点P且互相垂直的两条直线，其中l1交圆C2于A、B两点，l2交椭圆C1于另一点D．
（1）求椭圆C1的方程；
（2）求△ABD面积的最大值时直线l1的方程．
+
=1（a＞b＞0）的一个顶点，C1的长轴是圆C2：x2+y2=4的直径，l1，l2是过点P且互相垂直的两条直线，其中l1交圆C2于A、B两点，l2交椭圆C1于另一点D．（1）求椭圆C1的方程；
（2）求△ABD面积的最大值时直线l1的方程．
22．已知a∈R，函数f（x）=x3﹣3x2+3ax﹣3a+3．
（1）求曲线y=f（x）在点（1，f（1））处的切线方程；
（2）当x∈[0，2]时，求|f（x）|的最大值．
（1）求曲线y=f（x）在点（1，f（1））处的切线方程；
（2）当x∈[0，2]时，求|f（x）|的最大值．
