全一卷
1.已知全集 ,集合
,集合 ,则
,则 ()
()
 ,集合
,集合 ,则
,则 ()
()A. | B. | C. | D. |
2. 为虚数单位,则
为虚数单位,则 ( )
( )
 为虚数单位,则
为虚数单位,则 ( )
( )A.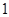 | B. | C. | D. |
3.命题“ ,
, ”的否定是()
”的否定是()
 ,
, ”的否定是()
”的否定是()A. , , | B. , , |
C. , , | D. , , |
4.若变量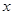 、
、 满足约束条件
满足约束条件 ,则
,则 的最大值是()
的最大值是()
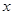 、
、 满足约束条件
满足约束条件 ,则
,则 的最大值是()
的最大值是()| A.2 | B.4 | C.7 | D.8 |
5.随机投掷两枚均匀的投骰子,他们向上的点数之和不超过5的概率为 ,点数之和大于5的概率为
,点数之和大于5的概率为 ,点数之和为偶数的概率为
,点数之和为偶数的概率为 ,则()
,则()
 ,点数之和大于5的概率为
,点数之和大于5的概率为 ,点数之和为偶数的概率为
,点数之和为偶数的概率为 ,则()
,则()A. | B. | C. | D. |
6.根据如下样本数据:
得到的回归方程为 ,则( )
,则( )
A. ,
, B.
B. ,
,
C. ,
, D.
D. ,
,
 | 3 | 4 | 5 | 6 | 7 | 8 |
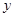 | 4.0 | 2.5 |  | 0.5 |  |  |
得到的回归方程为
 ,则( )
,则( )A.
 ,
, B.
B. ,
,
C.
 ,
, D.
D. ,
,
7.在如图所示的空间直角坐标系 中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为( )
中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为( )

 中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为( )
中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为( )
| A.①和② | B.③和① | C.④和③ | D.④和② |
8.设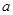 、
、 是关于
是关于 的方程
的方程 的两个不等实根,则过
的两个不等实根,则过 ,
, 两点的直线与双曲线
两点的直线与双曲线 的公共点的个数为( )
的公共点的个数为( )
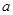 、
、 是关于
是关于 的方程
的方程 的两个不等实根,则过
的两个不等实根,则过 ,
, 两点的直线与双曲线
两点的直线与双曲线 的公共点的个数为( )
的公共点的个数为( )| A.0 | B.1 | C.2 | D.3 |
9.已知 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, ,则函数
,则函数 的零点的集合为( )
的零点的集合为( )
 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, ,则函数
,则函数 的零点的集合为( )
的零点的集合为( )A. | B. | C. | D. |
10.《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“盖”的术:置如其周,令相承也.又以高乘之,三十六成一.该术相当于给出了有圆锥的底面周长 与高
与高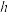 ,计算其体积
,计算其体积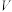 的近似公式
的近似公式 它实际上是将圆锥体积公式中的圆周率
它实际上是将圆锥体积公式中的圆周率 近似取为3.那么近似公式
近似取为3.那么近似公式 相当于将圆锥体积公式中的
相当于将圆锥体积公式中的 近似取为
近似取为
 与高
与高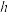 ,计算其体积
,计算其体积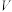 的近似公式
的近似公式 它实际上是将圆锥体积公式中的圆周率
它实际上是将圆锥体积公式中的圆周率 近似取为3.那么近似公式
近似取为3.那么近似公式 相当于将圆锥体积公式中的
相当于将圆锥体积公式中的 近似取为
近似取为A. | B. | C. | D. |
11.甲、乙两套设备生产的同类产品共4800件,采用分层抽样的方法从中抽取一个容量为80 的样本进行检测.若样本中有50件产品由甲设备生产,则乙设备生产的产品总数为________ 件.
12.若向量 ,
, ,
, ,则
,则
________ .
 ,
, ,
, ,则
,则
13.在 中,角
中,角 、
、 、
、 所对的边分别为
所对的边分别为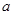 、
、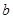 、
、 ,已知
,已知 ,
, ,
, ,则
,则
________ .
 中,角
中,角 、
、 、
、 所对的边分别为
所对的边分别为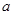 、
、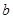 、
、 ,已知
,已知 ,
, ,
, ,则
,则
14.阅读如图所示的程序框图,运行相应的程序,若输入 的值为9,则输出
的值为9,则输出 的值为
的值为_______ .

 的值为9,则输出
的值为9,则输出 的值为
的值为
15.如图所示,函数 的图象由两条射线和三条线段组成.若
的图象由两条射线和三条线段组成.若 ,
, ,则正实数
,则正实数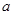 的取值范围是
的取值范围是________ .

 的图象由两条射线和三条线段组成.若
的图象由两条射线和三条线段组成.若 ,
, ,则正实数
,则正实数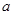 的取值范围是
的取值范围是
16.某项研究表明,在考虑行车安全的情况下,某路段车流量 (单位时间内测量点的车辆数,单位:辆/小时)与车流速度
(单位时间内测量点的车辆数,单位:辆/小时)与车流速度 (假设车辆以相同速度
(假设车辆以相同速度 行驶,单位:米/秒)平均车长
行驶,单位:米/秒)平均车长 (单位:米)的值有关,其公式为
(单位:米)的值有关,其公式为
(1)如果不限定车型, ,则最大车流量为
,则最大车流量为_______ 辆/小时;
(2)如果限定车型, ,则最大车流量比(1)中的最大车流量增加
,则最大车流量比(1)中的最大车流量增加______ 辆/小时.
 (单位时间内测量点的车辆数,单位:辆/小时)与车流速度
(单位时间内测量点的车辆数,单位:辆/小时)与车流速度 (假设车辆以相同速度
(假设车辆以相同速度 行驶,单位:米/秒)平均车长
行驶,单位:米/秒)平均车长 (单位:米)的值有关,其公式为
(单位:米)的值有关,其公式为
(1)如果不限定车型,
 ,则最大车流量为
,则最大车流量为(2)如果限定车型,
 ,则最大车流量比(1)中的最大车流量增加
,则最大车流量比(1)中的最大车流量增加17.已知圆 和点
和点 ,若定点
,若定点 和常数
和常数 满足:对圆
满足:对圆 上那个任意一点
上那个任意一点 ,都有
,都有 ,则:
,则:
(1)
________ ;
(2)
_________ .
 和点
和点 ,若定点
,若定点 和常数
和常数 满足:对圆
满足:对圆 上那个任意一点
上那个任意一点 ,都有
,都有 ,则:
,则:(1)

(2)

18.某实验室一天的温度(单位: )随时间
)随时间 (单位:
(单位: )的变化近似满足函数关系;
)的变化近似满足函数关系;
 .
.
(1)求实验室这一天上午8时的温度;
(2)求实验室这一天的最大温差.
 )随时间
)随时间 (单位:
(单位: )的变化近似满足函数关系;
)的变化近似满足函数关系; .
.(1)求实验室这一天上午8时的温度;
(2)求实验室这一天的最大温差.
19.已知等差数列 满足:
满足: ,且
,且 、
、 、
、 成等比数列.
成等比数列.
(1)求数列 的通项公式.
的通项公式.
(2)记 为数列
为数列 的前
的前 项和,是否存在正整数
项和,是否存在正整数 ,使得
,使得 若存在,求
若存在,求 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
 满足:
满足: ,且
,且 、
、 、
、 成等比数列.
成等比数列.(1)求数列
 的通项公式.
的通项公式.(2)记
 为数列
为数列 的前
的前 项和,是否存在正整数
项和,是否存在正整数 ,使得
,使得 若存在,求
若存在,求 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.20.如图,在正方体 中,
中, ,
, ,
, ,
, ,
, ,
, 分别是棱
分别是棱 ,
, ,
,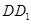 ,
,
 ,
, ,
, 的中点.求证:
的中点.求证:
(1)直线 ∥平面
∥平面 ;
;
(2)直线 ⊥平面
⊥平面 .
.
 中,
中, ,
, ,
, ,
, ,
, ,
, 分别是棱
分别是棱 ,
, ,
,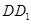 ,
, ,
, ,
, 的中点.求证:
的中点.求证:(1)直线
 ∥平面
∥平面 ;
;(2)直线
 ⊥平面
⊥平面 .
.
21.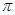 为圆周率,
为圆周率, 为自然对数的底数.
为自然对数的底数.
(1)求函数 的单调区间;
的单调区间;
(2)求 ,
, ,
, ,
, ,
, ,
, 这6个数中的最大数与最小数;
这6个数中的最大数与最小数;
(3)将 ,
, ,
, ,
, ,
, ,
, 这6个数按从小到大的顺序排列,并证明你的结论.
这6个数按从小到大的顺序排列,并证明你的结论.
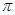 为圆周率,
为圆周率, 为自然对数的底数.
为自然对数的底数.(1)求函数
 的单调区间;
的单调区间;(2)求
 ,
, ,
, ,
, ,
, ,
, 这6个数中的最大数与最小数;
这6个数中的最大数与最小数;(3)将
 ,
, ,
, ,
, ,
, ,
, 这6个数按从小到大的顺序排列,并证明你的结论.
这6个数按从小到大的顺序排列,并证明你的结论.22.在平面直角坐标系 中,点
中,点 到点
到点 的距离比它到
的距离比它到 轴的距离多1,记点
轴的距离多1,记点 的轨迹为
的轨迹为 .
.
(1)求轨迹为 的方程
的方程
(2)设斜率为 的直线
的直线 过定点
过定点 ,求直线
,求直线 与轨迹
与轨迹 恰好有一个公共点,两个公共点,三个公共点时
恰好有一个公共点,两个公共点,三个公共点时 的相应取值范围.
的相应取值范围.
 中,点
中,点 到点
到点 的距离比它到
的距离比它到 轴的距离多1,记点
轴的距离多1,记点 的轨迹为
的轨迹为 .
.(1)求轨迹为
 的方程
的方程(2)设斜率为
 的直线
的直线 过定点
过定点 ,求直线
,求直线 与轨迹
与轨迹 恰好有一个公共点,两个公共点,三个公共点时
恰好有一个公共点,两个公共点,三个公共点时 的相应取值范围.
的相应取值范围. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
