搜索
全一卷
难度系数：0.40 
答案解析
有奖纠错
1．设
则
则
A． | B． |
C． | D． |
2．已知函数
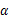若
=
若
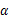=| A．0 | B．1 | C．2 | D．3 |
3．设i为虚数单位，则
等于（）
等于（）| A．-2-3i | B．-2+3i | C．2-3i | D．2+3i |
4．
某程序框图如图所示，若输出的S=57，则判断框内位
某程序框图如图所示，若输出的S=57，则判断框内位
| A．k＞4? | B．k＞5? |
| C．k＞6? | D．k＞7? |
5．设
，则“
”是“
”的
，则“
”是“
”的| A．充分而不必要条件 | B．必要而不充分条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
6．若实数x，y满足不等式组合
，则x+y的最大值为（ ）
，则x+y的最大值为（ ）| A．9 | B． | C．1 | D． |
7．若某几何体的三视图（单位：
如图所示，则此几何体的体积是 144 
．
如图所示，则此几何体的体积是 144 
．
A． cm3 | B． cm3 |
C． cm3 | D． cm3 |
8．已知
是函数
的一个零点，若
，则（ ）
是函数
的一个零点，若
，则（ ）A． , | B．, |
C． , | D．, |
9．（10）设O为坐标原点，
,
是双曲线
（a＞0，b＞0）的焦点，若在双曲线上存在点P，满足∠P=60°，∣OP∣=
,则该双曲线的渐近线方程为
,
是双曲线
（a＞0，b＞0）的焦点，若在双曲线上存在点P，满足∠P=60°，∣OP∣=
,则该双曲线的渐近线方程为A．x± y="0" | B．x±y=0 |
C．x± ="0" | D． ±y=0 |
10．设Sn为等比数列{an}的前n项和，8a2＋a5=0，则
=________ .
=11．（11）在如图所示的茎叶图中，甲、乙两组数据的中位数分别是 、
12．已知平面向量
则
的值是 。
则
的值是 。13．在如下数表中，已知每行、每列中的数都成等差数列，
那么，位于下表中的第n行第n+1列的数是_______
那么，位于下表中的第n行第n+1列的数是
14．若正实数X，Y 满足2X+Y+6=XY"，则XY 的最小值是______
15．某商家一月份至五月份累计销售额达3860万元，预测六月份销售额为500万元，七月份销售额比六月份递增x%，八月份销售额比七月份递增x%，九、十月份销售总额与七、八月份销售总额相等，若一月至十月份销售总额至少至少达7000万元，则，x 的最小值_______
16．在平行四边形
中，点
是对角线
和
的交点，
分别是线段
的中点，在
中任意取一点
，在
中任意取一点
，设点
满足向量
，则在上述点组成的集合中的点，落在平行四边形外（不含边界）的概率为__________ ．
中，点
是对角线
和
的交点，
分别是线段
的中点，在
中任意取一点
，在
中任意取一点
，设点
满足向量
，则在上述点组成的集合中的点，落在平行四边形外（不含边界）的概率为17．在△ABC中，角A，B，C所对的边分别为a,b,c,设S为△ABC的面积，满足
．
（Ⅰ）求角C的大小；
（Ⅱ）求
的最大值．
．（Ⅰ）求角C的大小；
（Ⅱ）求
的最大值．18．设
为实数，首项为
，公差为
的等差数列
的前n项和为
，满足
+15=0．
（Ⅰ）若
=5，求
及；
（Ⅱ）求的取值范围．
为实数，首项为，公差为的等差数列的前n项和为，满足+15=0．（Ⅰ）若
=5，求及；（Ⅱ）求
的取值范围．19．
如图，在平行四边形ABCD中，AB=2BC，∠ABC=120°．E为线段AB的中点，将△ADE沿直线DE翻折成△A’DE，使平面A’DE⊥平面BCD，F为线段A’C的中点．
（Ⅰ）求证：BF∥平面A’DE；
（Ⅱ）设M为线段DE的中点，求直线FM与平面A’DE所成角的余弦值．
如图，在平行四边形ABCD中，AB=2BC，∠ABC=120°．E为线段AB的中点，将△ADE沿直线DE翻折成△A’DE，使平面A’DE⊥平面BCD，F为线段A’C的中点．
（Ⅰ）求证：BF∥平面A’DE；
（Ⅱ）设M为线段DE的中点，求直线FM与平面A’DE所成角的余弦值．
20．已知m是非零实数，抛物线
（p>0）
的焦点F在直线
上．
（I）若m=2，求抛物线C的方程
（II）设直线
与抛物线C交于A、B，△A
,△
的重心分别为G,H
求证：对任意非零实数m,抛物线C的准线与x轴的焦点在以线段GH为直径的圆外．
（p>0）的焦点F在直线
上．（I）若m=2，求抛物线C的方程
（II）设直线
与抛物线C交于A、B，△A
,△
的重心分别为G,H求证：对任意非零实数m,抛物线C的准线与x轴的焦点在以线段GH为直径的圆外．
