全一卷
1.已知集合 ,则
,则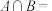
 ,则
,则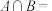
A. | B. | C.( | D. ) ) |
2.若复数 满足
满足 ,其中
,其中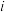 为虚数为单位,则
为虚数为单位,则 =
=
 满足
满足 ,其中
,其中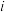 为虚数为单位,则
为虚数为单位,则 =
=A. | B. | C. | D. |
3.设 则
则 的大小关系是
的大小关系是
 则
则 的大小关系是
的大小关系是A. | B. | C. | D. |
4.要得到函数

 的图象,只需要将函数
的图象,只需要将函数 的图象
的图象


 的图象,只需要将函数
的图象,只需要将函数 的图象
的图象A.向左平移 个单位 个单位 |
B.向右平移 个单位 个单位 |
C.向左平移 个单位 个单位 |
D.向右平移 个单位 个单位 |
5.
设 ,命题“若
,命题“若 ,则方程
,则方程 有实根”的逆否命题是
有实根”的逆否命题是
A.若方程 有实根,则 有实根,则 |
B.若方程 有实根,则 有实根,则 |
C.若方程 没有实根,则 没有实根,则 |
D.若方程 没有实根,则 没有实根,则 |
6.在区间 上随机地取一个数
上随机地取一个数 ,则事件“
,则事件“ ”发生的概率为
”发生的概率为
 上随机地取一个数
上随机地取一个数 ,则事件“
,则事件“ ”发生的概率为
”发生的概率为A.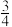 | B.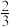 | C. | D.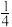 |
7.若函数 是奇函数,则使
是奇函数,则使 成立的
成立的 的取值范围为( )
的取值范围为( )
 是奇函数,则使
是奇函数,则使 成立的
成立的 的取值范围为( )
的取值范围为( )A.( ) ) | B.(-1,0) | C. | D. |
8.已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为
A. | B. | C. | D. |
9.设函数 ,若
,若 ,则
,则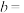
 ,若
,若 ,则
,则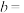
A. | B. | C.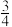 | D. |
10.为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:

①甲地该月14时的平均气温低于乙地该月14时的平均气温;
②甲地该月14时的平均气温高于乙地该月14时的平均气温;
③甲地该月14时的平均气温的标准差小于乙地该月14时的气温的标准差;
④甲地该月14时的平均气温的标准差大于乙地该月14时的气温的标准差.
其中根据茎叶图能得到的统计结论的标号为__________ .

①甲地该月14时的平均气温低于乙地该月14时的平均气温;
②甲地该月14时的平均气温高于乙地该月14时的平均气温;
③甲地该月14时的平均气温的标准差小于乙地该月14时的气温的标准差;
④甲地该月14时的平均气温的标准差大于乙地该月14时的气温的标准差.
其中根据茎叶图能得到的统计结论的标号为
11.执行右边的程序框图,若输入的 的值为
的值为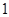 ,则输出的
,则输出的 的值是 .
的值是 . 
 的值为
的值为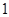 ,则输出的
,则输出的 的值是 .
的值是 . 
12.若 满足约束条件
满足约束条件 则
则 的最大值为
的最大值为_______ .
 满足约束条件
满足约束条件 则
则 的最大值为
的最大值为13.过点 作圆
作圆 的两条切线,切点分别为
的两条切线,切点分别为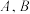 ,则
,则 = .
= .
 作圆
作圆 的两条切线,切点分别为
的两条切线,切点分别为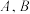 ,则
,则 = .
= .14.定义运算“ ”:
”:  (
( ).当
).当 时,
时, 的最小值是
的最小值是_______ .
 ”:
”:  (
( ).当
).当 时,
时, 的最小值是
的最小值是15.过双曲线

 的右焦点作一条与其渐近线平行的直线,交
的右焦点作一条与其渐近线平行的直线,交 于点
于点 .若点
.若点 的横坐标为
的横坐标为 ,则
,则 的离心率为 .
的离心率为 .


 的右焦点作一条与其渐近线平行的直线,交
的右焦点作一条与其渐近线平行的直线,交 于点
于点 .若点
.若点 的横坐标为
的横坐标为 ,则
,则 的离心率为 .
的离心率为 .16.某中学调查了某班全部 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
(1)从该班随机选 名同学,求该同学至少参加上述一个社团的概率;
名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的 名同学中,有5名男同学
名同学中,有5名男同学
 名女同学
名女同学 现从这
现从这 名男同学和
名男同学和 名女同学中各随机选
名女同学中各随机选 人,求
人,求 被选中且
被选中且 未被选中的概率.
未被选中的概率.
 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)| 参加书法社团 | 未参加书法社团 | |
| 参加演讲社团 |  |  |
| 未参加演讲社团 |  |  |
(1)从该班随机选
 名同学,求该同学至少参加上述一个社团的概率;
名同学,求该同学至少参加上述一个社团的概率;(2)在既参加书法社团又参加演讲社团的
 名同学中,有5名男同学
名同学中,有5名男同学
 名女同学
名女同学 现从这
现从这 名男同学和
名男同学和 名女同学中各随机选
名女同学中各随机选 人,求
人,求 被选中且
被选中且 未被选中的概率.
未被选中的概率.17.(本小题满分12分) 中,角
中,角 所对的边分别为
所对的边分别为 .已知
.已知 求
求 和
和 的值.
的值.
 中,角
中,角 所对的边分别为
所对的边分别为 .已知
.已知 求
求 和
和 的值.
的值.18.如图,三棱台 中,
中,  分别为
分别为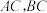 的中点.
的中点.

(Ⅰ)求证: 平面
平面  ;
;
(Ⅱ)若 求证:平面
求证:平面 平面
平面  .
.
 中,
中,  分别为
分别为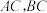 的中点.
的中点.
(Ⅰ)求证:
 平面
平面  ;
;(Ⅱ)若
 求证:平面
求证:平面 平面
平面  .
.19.已知数列 是首项为正数的等差数列,数列
是首项为正数的等差数列,数列 的前
的前 项和为
项和为 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
 是首项为正数的等差数列,数列
是首项为正数的等差数列,数列 的前
的前 项和为
项和为 .
.(1)求数列
 的通项公式;
的通项公式;(2)设
 ,求数列
,求数列 的前
的前 项和
项和 .
.20.设函数 . 已知曲线
. 已知曲线 在点
在点 处的切线与直线
处的切线与直线 平行.
平行.
(Ⅰ)求 的值;
的值;
(Ⅱ)是否存在自然数 ,使得方程
,使得方程 在
在 内存在唯一的根?如果存在,求出
内存在唯一的根?如果存在,求出 ;如果不存在,请说明理由;
;如果不存在,请说明理由;
(Ⅲ)设函数 (
( 表示,
表示,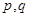 中的较小值),求
中的较小值),求 的最大值.
的最大值.
 . 已知曲线
. 已知曲线 在点
在点 处的切线与直线
处的切线与直线 平行.
平行.(Ⅰ)求
 的值;
的值;(Ⅱ)是否存在自然数
 ,使得方程
,使得方程 在
在 内存在唯一的根?如果存在,求出
内存在唯一的根?如果存在,求出 ;如果不存在,请说明理由;
;如果不存在,请说明理由;(Ⅲ)设函数
 (
( 表示,
表示,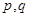 中的较小值),求
中的较小值),求 的最大值.
的最大值.21.平面直角坐标系 中,已知椭圆
中,已知椭圆 :
: 的离心率为
的离心率为 ,且点(
,且点( ,
, )在椭圆
)在椭圆 上.
上.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设椭圆 :
: ,
, 为椭圆
为椭圆 上任意一点,过点
上任意一点,过点 的直线
的直线 交椭圆
交椭圆 于
于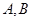 两点,射线
两点,射线 交椭圆
交椭圆 于点
于点 .
.
(ⅰ)求 的值;
的值;
(ⅱ)求 面积的最大值.
面积的最大值.
 中,已知椭圆
中,已知椭圆 :
: 的离心率为
的离心率为 ,且点(
,且点( ,
, )在椭圆
)在椭圆 上.
上.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)设椭圆
 :
: ,
, 为椭圆
为椭圆 上任意一点,过点
上任意一点,过点 的直线
的直线 交椭圆
交椭圆 于
于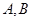 两点,射线
两点,射线 交椭圆
交椭圆 于点
于点 .
.(ⅰ)求
 的值;
的值;(ⅱ)求
 面积的最大值.
面积的最大值. 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
