搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．已知a,b都是实数，那么“
”是“a>b”的
”是“a>b”的| A．充分而不必要条件 | B．必要而不充分条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
2．在(x-1)(x-2)(x-3)(x-4)(x-5)的展开式中，含
的项的系数是
的项的系数是| A．-15 | B．85 | C．-120 | D．274 |
3．在同一平面直角坐标系中，函数y＝cos(
＋
)(x∈[0,2π])的图象和直线y＝
的交点个数是( )
＋)(x∈[0,2π])的图象和直线y＝的交点个数是( )| A．0 | B．1 | C．2 | D．4 |
4．若双曲线
的两个焦点到一条准线的距离之比为3：2，则双曲线的离心率是
的两个焦点到一条准线的距离之比为3：2，则双曲线的离心率是| A．3 | B．5 | C． | D． |
5．已知
是实数，
是纯虚数，则=（）
是实数，
是纯虚数，则=（）| A．1 | B．-1 | C． | D．- |
6．已知U=R，A=
，B=
，则
( )
，B=
，则
( )A． | B． |
C． | D． |
7．若
则
=( )
则
=( )A． | B．2 | C． | D． |
8．已知
，
是平面内两个互相垂直的单位向量，若向量
满足
，则
的最大值是( )
，
是平面内两个互相垂直的单位向量，若向量
满足
，则
的最大值是( )| A．1 | B．2 | C． | D． |
9．如图，AB是平面
的斜线段，A为斜足，若点P在平面内运动，使得△ABP的面积为定值，则动点P的轨迹是
的斜线段，A为斜足，若点P在平面内运动，使得△ABP的面积为定值，则动点P的轨迹是
| A．圆 | B．椭圆 |
| C．一条直线 | D．两条平行直线 |
10．已知F1、F2为椭圆
的两个焦点，过F1的直线交椭圆于A、B两点
若|F2A|+|F2B|=12，则|AB|= 。
的两个焦点，过F1的直线交椭圆于A、B两点若|F2A|+|F2B|=12，则|AB|= 。
11．在△ABC中，角A、B、C所对的边分别为a、b、c。若
则cos A= .
则cos A= .12．如图，已知球O的面上四点
，DA⊥平面ABC。AB⊥BC，DA=AB=BC=
，则球O的体积等于 。
，DA⊥平面ABC。AB⊥BC，DA=AB=BC=，则球O的体积等于 。
13．用1，2，3，4，5，6组成六位数（没有重复数字），要求任何相邻两个数字的奇偶性不同，且1和2相邻。这样的六位数的个数是 （用数字作答）
14．已知t为常数，函数
在区间[0，3]上的最大值为2，则
_____________
在区间[0，3]上的最大值为2，则15．>0，若平面内三点A（1，-），B（2，
），C（3，
）共线，则=_______。
>0，若平面内三点A（1，-），B（2，
），C（3，
）共线，则=_______。16．若
，且当
时，恒有
，则以
,b为坐标点P（，
b）所形成的平面区域的面积等于____________。
，且当
时，恒有
，则以
,b为坐标点P（，b）所形成的平面区域的面积等于____________。
17．（本题15分）已知曲线C是到点
和到直线
距离相等的点的轨迹，l是过点Q（-1，0）的直线，
M是C上（不在l上）的动点；A、B在l上，
轴（如图）。
（Ⅰ）求曲线C的方程；
（Ⅱ）求出直线l的方程，使得
为常数。
和到直线
距离相等的点的轨迹，l是过点Q（-1，0）的直线，M是C上（不在l上）的动点；A、B在l上，
轴（如图）。
（Ⅰ）求曲线C的方程；
（Ⅱ）求出直线l的方程，使得
为常数。18．已知数列
，
，
，
．记：
．
求证：当
时，
（1）
；
（2）
；
（3）
．
，
，
，
．记：
．求证：当
时，（1）
；（2）
；（3）
．19．如图所示，矩形ABCD和梯形BEFC所在平面互相垂直，
BE∥CF，∠BCF=∠CEF=90°,AD=
,EF=2.
(1)求证:AE∥平面DCF;
(2)当AB的长为何值时,二面角A—EF—C的大小为60°?
BE∥CF，∠BCF=∠CEF=90°,AD=
,EF=2.(1)求证:AE∥平面DCF;
(2)当AB的长为何值时,二面角A—EF—C的大小为60°?
20．已知
是实数，函数
.
⑴求函数f(x)的单调区间；
⑵设g(x)为f(x)在区间
上的最小值.
（i）写出g(a)的表达式；（ii）求的取值范围，使得
.
是实数，函数
.⑴求函数f(x)的单调区间；
⑵设g(x)为f(x)在区间
上的最小值.（i）写出g(a)的表达式；（ii）求
的取值范围，使得
.21．一个袋中有若干个大小相同的黑球、白球和红球．已知从袋中任意摸出1个球，得到黑球的概率是
；从袋中任意摸出2个球，至少得到1个白球的概率是
．
（Ⅰ）若袋中共有10个球，
（i）求白球的个数；
（ii）从袋中任意摸出3个球，记得到白球的个数为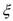
，求随机变量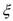的数学期望
．
（Ⅱ）求证：从袋中任意摸出2个球，至少得到1个黑球的概率不大于
．并指出袋中哪种颜色的球个数最少．
；从袋中任意摸出2个球，至少得到1个白球的概率是
．（Ⅰ）若袋中共有10个球，
（i）求白球的个数；
（ii）从袋中任意摸出3个球，记得到白球的个数为
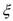，求随机变量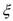的数学期望
．（Ⅱ）求证：从袋中任意摸出2个球，至少得到1个黑球的概率不大于
．并指出袋中哪种颜色的球个数最少．