全一卷
1.函数 的递增区间是______.
的递增区间是______.
 的递增区间是______.
的递增区间是______.2.若方程 有实数解,则
有实数解,则 的取值范围是
的取值范围是______ .
 有实数解,则
有实数解,则 的取值范围是
的取值范围是3.在坐标平面上,方程 的图象与
的图象与 轴所围成图形的面积为______.
轴所围成图形的面积为______.
 的图象与
的图象与 轴所围成图形的面积为______.
轴所围成图形的面积为______.4.把数列 依次按一项、二项、三项、四项循环分为
依次按一项、二项、三项、四项循环分为 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,…,在第100个括号内的最后一个数字为_________.
,…,在第100个括号内的最后一个数字为_________.
 依次按一项、二项、三项、四项循环分为
依次按一项、二项、三项、四项循环分为 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,…,在第100个括号内的最后一个数字为_________.
,…,在第100个括号内的最后一个数字为_________.5. 条抛物线
条抛物线 ,将平面
,将平面 最多分成______部分.
最多分成______部分.
 条抛物线
条抛物线 ,将平面
,将平面 最多分成______部分.
最多分成______部分.6.已知 分别是单位圆的直径与弦,且
分别是单位圆的直径与弦,且 ,
, ,
, 是
是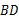 的中点,连结
的中点,连结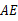 ,与
,与 交于
交于 点,延长
点,延长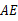 ,与圆交于
,与圆交于 点;又连结
点;又连结 ,与
,与 交于
交于 点.
点.
(1)试证: .
.
(2)求四边形 的面积.
的面积.
 分别是单位圆的直径与弦,且
分别是单位圆的直径与弦,且 ,
, ,
, 是
是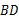 的中点,连结
的中点,连结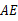 ,与
,与 交于
交于 点,延长
点,延长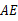 ,与圆交于
,与圆交于 点;又连结
点;又连结 ,与
,与 交于
交于 点.
点.(1)试证:
 .
.(2)求四边形
 的面积.
的面积.7.设正实数 ,自然数
,自然数 ,且方程
,且方程 恰有
恰有 个不同的解.试求
个不同的解.试求 的取值范围.(
的取值范围.( 表示不超过
表示不超过 的最大整数)
的最大整数)
 ,自然数
,自然数 ,且方程
,且方程 恰有
恰有 个不同的解.试求
个不同的解.试求 的取值范围.(
的取值范围.( 表示不超过
表示不超过 的最大整数)
的最大整数)8.设整数 是区间
是区间 中的不同整数.证明:集合
中的不同整数.证明:集合 有这样的子集存在,它的所有元素之和能被
有这样的子集存在,它的所有元素之和能被 整除.
整除.
 是区间
是区间 中的不同整数.证明:集合
中的不同整数.证明:集合 有这样的子集存在,它的所有元素之和能被
有这样的子集存在,它的所有元素之和能被 整除.
整除. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
