搜索
全一卷
难度系数：0.65 
答案解析
有奖纠错
1．设
，
，
是实数.那么对任何实数
，不等式
都成立的充分必要条件是（ ）
，
，
是实数.那么对任何实数
，不等式
都成立的充分必要条件是（ ）A．，同时为0，且 | B． |
C． | D． |
2．给出下列两个命题：（1）设，，都是复数。如果
，则
；（2）设，，都是复数，如果，则。那么，下述说法正确的是（ ）
，，都是复数。如果
，则
；（2）设，，都是复数，如果，则。那么，下述说法正确的是（ ）| A．命题（1）正确，命题（2）也正确 | B．命题（1）正确，命题（2）错误 |
| C．命题（1）错误，命题（2）也错误 | D．命题（1）错误，命题（2）正确 |
3．已知数列
满足
，且
，其前n项之和为
，则满足不等式
的最小整数n是
满足
，且
，其前n项之和为
，则满足不等式
的最小整数n是| A．5 | B．6 | C．7 | D．8 |
4．已知
，
，则下列三数：
，
的大小关系是（ ）。
，
，则下列三数：
，
的大小关系是（ ）。A． | B． | C． | D． |
5．在正
棱锥中，相邻两侧面所成的二面角的取值范围是（ ）
棱锥中，相邻两侧面所成的二面角的取值范围是（ ）A． | B． | C． | D． |
6．在平面直角坐标系中，方程
（为，为不相等的两个正数）所代表的曲线是（ ）
（为，为不相等的两个正数）所代表的曲线是（ ）| A．三角形 | B．正方形 | C．非正方形的长方形 | D．非正方形的菱形 |
7．已知有向线段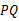
的起点
和终点
的坐标分别为
和
。若直线
：
与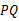的延长线相交，则
的取值范围是______。
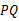的起点
和终点
的坐标分别为
和
。若直线
：
与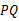的延长线相交，则
的取值范围是______。8．已知
，
，且
，
.则
的值为_____________。
，
，且
，
.则
的值为_____________。9．已知点集
，
。则点集
中的整点（即横、纵坐标均为整数的点）的个数是______。
，
。则点集
中的整点（即横、纵坐标均为整数的点）的个数是______。10．设
，则
的最大值是______。
，则
的最大值是______。11．已知一平面与一正方体的12条棱的所成角都等于α，则sinα=______．
12．已知95个数
，
，…，
，每个都只能取
或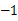
两个值之一。那么，它们两两之积的和
的最小正值是______。
，
，…，
，每个都只能取
或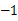
两个值之一。那么，它们两两之积的和
的最小正值是______。13．
的二次方程
中，
，
，
均是复数，且
，设这个方程的两个根
，
满足
，求
的最大值和最小值．
的二次方程
中，
，
，
均是复数，且
，设这个方程的两个根
，
满足
，求
的最大值和最小值．14．将与105互素的所有正整数从小到大排成数列。试求出这个数列的第1000项。
15．如图，设
的外接圆
的半径为
，内心为
，
，
，
的外角平分线交圆于
。证明：
（1）
；
（2）
。
的外接圆
的半径为
，内心为
，
，
，
的外角平分线交圆于
。证明：
（1）
；（2）
。16．给定平面上的点集
，中任三点均不共线。将中所有的点任意分成83组，使得每组至少有3个点，且每点恰好属于一组，然后将在同一组的任两点用一条线段相连，不在同一组的两点不连线段，这样得到一个图案
。不同的分组方式得到不同的图案。将图案中所含的以中的点为顶点的三角形的个数记为
。
（1）求的最小值
；
（2）设
是使
的一个图案，若将中的线段（指以的点为端点的线段）用4种颜色染色，每条线段恰好染一种颜色。证明存在一个染色方案，使染色后不含以的点为顶点的三边颜色相同的三角形。
，中任三点均不共线。将中所有的点任意分成83组，使得每组至少有3个点，且每点恰好属于一组，然后将在同一组的任两点用一条线段相连，不在同一组的两点不连线段，这样得到一个图案
。不同的分组方式得到不同的图案。将图案中所含的以中的点为顶点的三角形的个数记为
。（1）求
的最小值
；（2）设
是使
的一个图案，若将中的线段（指以的点为端点的线段）用4种颜色染色，每条线段恰好染一种颜色。证明存在一个染色方案，使染色后不含以的点为顶点的三边颜色相同的三角形。