全一卷
1.设集合A={x∣log2x<1}, B={X∣ <1}, 则A
<1}, 则A = .
= .
 <1}, 则A
<1}, 则A = .
= .2.已知(1+ax)3,=1+10x+bx3+…+a3x3,则b= .
3.甲、乙、丙三人将参加某项测试,他们能达标的概率分别是0.8、0.6、0.5,则三人都达标的概率是___________ ,三人中至少有一人达标的概率是_________ .
4.过原点作圆 的两条切线,切点分别为
的两条切线,切点分别为 ,
, ,则线段
,则线段 的长为 .
的长为 .
 的两条切线,切点分别为
的两条切线,切点分别为 ,
, ,则线段
,则线段 的长为 .
的长为 .5.下图是样本容量为200的频率分布直方图。根据样本的频率分布直方图估计,样本数据落在【6,10】内的频数为 ,数据落在(2,10)内的概率约为 。w.w.w.k.s.5.u.c.o.m 





6.如图,过抛物线y2=2PX(P>0)的焦点F的直线与抛物线相交于M、N两点,自M、N向准线L作垂线,垂足分别为M1、N1

(Ⅰ)求证:FM1⊥FN1:
(Ⅱ)记△FMM1、、△FM1N1、△FN N1的面积分别为 ,试判断S22=4S1S3是否成立,并证明你的结论。
,试判断S22=4S1S3是否成立,并证明你的结论。

(Ⅰ)求证:FM1⊥FN1:
(Ⅱ)记△FMM1、、△FM1N1、△FN N1的面积分别为
 ,试判断S22=4S1S3是否成立,并证明你的结论。
,试判断S22=4S1S3是否成立,并证明你的结论。7.在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且
(Ⅰ)确定角C的大小:
(Ⅱ)若c= ,且△ABC的面积为
,且△ABC的面积为
 ,求a+b的值.
,求a+b的值.

(Ⅰ)确定角C的大小:
(Ⅱ)若c=
 ,且△ABC的面积为
,且△ABC的面积为
 ,求a+b的值.
,求a+b的值.8.如图,四棱锥 的底面是正方形,
的底面是正方形, 平面
平面 ,
, ,点
,点 是
是 上的点,且
上的点,且 .
.
(1)求证:对任意的 ,都有
,都有 ;
;
(2)若二面角 的大小为
的大小为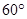 ,求
,求 的.
的.

 的底面是正方形,
的底面是正方形, 平面
平面 ,
, ,点
,点 是
是 上的点,且
上的点,且 .
. (1)求证:对任意的
 ,都有
,都有 ;
;(2)若二面角
 的大小为
的大小为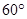 ,求
,求 的.
的.
9.已知{an}是一个公差大于0的等差数列,且满足a3a6=55, a2+a7=16.
(Ⅰ)求数列{an}的通项公式:
(Ⅱ)若数列{an}和数列{bn}满足等式:an= ,求数列{bn}的前n项和Sn
,求数列{bn}的前n项和Sn
(Ⅰ)求数列{an}的通项公式:
(Ⅱ)若数列{an}和数列{bn}满足等式:an=
 ,求数列{bn}的前n项和Sn
,求数列{bn}的前n项和Sn10.(本小题满分14分)已知关于x的函数f(x)= +bx2+cx+bc,其导函数为f+(x)。令g(x)=∣f+(x) ∣,记函数g(x)在区间[-1、1]上的最大值为M。
+bx2+cx+bc,其导函数为f+(x)。令g(x)=∣f+(x) ∣,记函数g(x)在区间[-1、1]上的最大值为M。
(Ⅰ)如果函数f(x)在x=1处有极值- ,试确定b、c的值;
,试确定b、c的值;
(Ⅱ)若∣b∣>1,证明对任意的c,都有M>2;
(Ⅲ)若M≥K对任意的b、c恒成立,试求k的最大值。
 +bx2+cx+bc,其导函数为f+(x)。令g(x)=∣f+(x) ∣,记函数g(x)在区间[-1、1]上的最大值为M。
+bx2+cx+bc,其导函数为f+(x)。令g(x)=∣f+(x) ∣,记函数g(x)在区间[-1、1]上的最大值为M。(Ⅰ)如果函数f(x)在x=1处有极值-
 ,试确定b、c的值;
,试确定b、c的值;(Ⅱ)若∣b∣>1,证明对任意的c,都有M>2;
(Ⅲ)若M≥K对任意的b、c恒成立,试求k的最大值。
11.围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元).设修建此矩形场地围墙的总费用为y.

(Ⅰ)将y表示为x的函数;
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.

(Ⅰ)将y表示为x的函数;
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
12.若向量 ,则
,则 ( )
( )
 ,则
,则 ( )
( )A. | B. | C. | D. |
13.函数 的反函数是()
的反函数是()
 的反函数是()
的反函数是()A. | B. |
C. | D. |
14.“sin =
= ”是“
”是“ ”
” 的 ( )
的 ( )
 =
= ”是“
”是“ ”
” 的 ( )
的 ( )| A.充分而不必要条件 | B.必要而不充分条件 | C.充要条件 | D.既不充分也不必要条件 |
15.从5名志愿者中选派4人在星期五、星期六、星期日参加公益活动,每人一天,要求星期五有一人参加,星期六有两人参加,星期日有一人参加,则不同的选派方法共有()
| A.120种 | B.96种 | C.60种 | D.48种 |
16.已知双曲线 (b>0)的焦点,则b=()
(b>0)的焦点,则b=()
 (b>0)的焦点,则b=()
(b>0)的焦点,则b=()| A.3 | B. | C. | D. |
17.如图,在三棱柱ABC-A1B1C1中,∠ACB=900,∠ACC1=600,∠BCC1=450,侧棱CC1的长为1,则该三棱柱的高等于()

A. | B. | C.  | D. |
18.设 记不超过
记不超过 的最大整数为[
的最大整数为[ ],令{
],令{ }=
}= -[
-[ ],则
],则 {
{ },[
},[ ],
], ()
()
 记不超过
记不超过 的最大整数为[
的最大整数为[ ],令{
],令{ }=
}= -[
-[ ],则
],则 {
{ },[
},[ ],
], ()
()| A.是等差数列但不是等比数列 | B.是等比数列但不是等差数列 |
| C.既是等差数列又是等比数列 | D.既不是等差数列也不是等比数列 |
19.函数 的图像F按向量a平移到F/,F/的解析式y=f(x),当y=f(x)为奇函数时,向量a可以等于
的图像F按向量a平移到F/,F/的解析式y=f(x),当y=f(x)为奇函数时,向量a可以等于
 的图像F按向量a平移到F/,F/的解析式y=f(x),当y=f(x)为奇函数时,向量a可以等于
的图像F按向量a平移到F/,F/的解析式y=f(x),当y=f(x)为奇函数时,向量a可以等于A. | B. | C. | D. |
 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
