全一卷
1.已知 且
且 ,则
,则 的取值范围是 .(答案用区间表示)
的取值范围是 .(答案用区间表示)
 且
且 ,则
,则 的取值范围是 .(答案用区间表示)
的取值范围是 .(答案用区间表示)2.三张卡片上分别写上字母E、E、B,将三张卡片随机地排成一行,恰好排成英文单词BEE的概率为 。.C#
3.设 为等差数列
为等差数列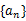 的前
的前 项和,若
项和,若 ,则
,则 。
。
 为等差数列
为等差数列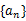 的前
的前 项和,若
项和,若 ,则
,则 。
。4.如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.

5.已知集合 ,
, ,则
,则 ( )
( )
 ,
, ,则
,则 ( )
( )A. | B. | C. | D. |
6.设a,b为实数,若复数 ,则
,则
 ,则
,则A. | B. |
C. | D. |
7.设 为等比数列
为等比数列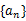 的前n项和,已知
的前n项和,已知 ,则公比
,则公比 ( )
( )
 为等比数列
为等比数列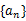 的前n项和,已知
的前n项和,已知 ,则公比
,则公比 ( )
( )| A.3 | B.4 | C.5 | D.6 |
8.已知 ,函数
,函数 ,若
,若 满足关于
满足关于 的方程
的方程 ,则下列选项的命题中为假命题的是
,则下列选项的命题中为假命题的是
 ,函数
,函数 ,若
,若 满足关于
满足关于 的方程
的方程 ,则下列选项的命题中为假命题的是
,则下列选项的命题中为假命题的是A. | B. |
C. | D. |
9.如果执行下面的程序框图,输入 ,那么输出的
,那么输出的 等于
等于

 ,那么输出的
,那么输出的 等于
等于
| A.720 | B.360 | C.240 | D.120 |
10.设 >0,函数y=sin(
>0,函数y=sin( x+
x+ )+2的图象向右平移
)+2的图象向右平移 个单位后与原图象重合,则
个单位后与原图象重合,则 的最小值是
的最小值是
 >0,函数y=sin(
>0,函数y=sin( x+
x+ )+2的图象向右平移
)+2的图象向右平移 个单位后与原图象重合,则
个单位后与原图象重合,则 的最小值是
的最小值是A.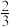 | B.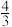 | C. | D.3 |
11.设抛物线y2=8x的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A为垂足.如
果直线AF的斜率为 ,那么|PF|=
,那么|PF|=
果直线AF的斜率为
 ,那么|PF|=
,那么|PF|=A. | B.8 | C. | D.16 |
12.平面上 三点不共线,设
三点不共线,设 ,则
,则 的面积等于.C#
的面积等于.C#
 三点不共线,设
三点不共线,设 ,则
,则 的面积等于.C#
的面积等于.C#A. | B. |
C. | D. |
13.设双曲的一个焦点为 ,虚轴的一个端点为
,虚轴的一个端点为 ,如果直线
,如果直线 与该双曲线的一条渐近线垂直,那么此双曲线的离心率为
与该双曲线的一条渐近线垂直,那么此双曲线的离心率为
 ,虚轴的一个端点为
,虚轴的一个端点为 ,如果直线
,如果直线 与该双曲线的一条渐近线垂直,那么此双曲线的离心率为
与该双曲线的一条渐近线垂直,那么此双曲线的离心率为A.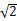 | B. | C. | D. |
14.设2a=5b=m,且 ,则m等于( )
,则m等于( )
 ,则m等于( )
,则m等于( )A. | B.10 | C.20 | D.100 |
15.已知 是球
是球 表面上的点,
表面上的点, ,
, ,
, ,
, ,则球
,则球 表面积等于
表面积等于
 是球
是球 表面上的点,
表面上的点, ,
, ,
, ,
, ,则球
,则球 表面积等于
表面积等于A.4 | B.3 | C.2 | D. |
16.已知点P在曲线y= 上,a为曲线在点P处的切线的倾斜角,则a的取值
上,a为曲线在点P处的切线的倾斜角,则a的取值
范围是( )
 上,a为曲线在点P处的切线的倾斜角,则a的取值
上,a为曲线在点P处的切线的倾斜角,则a的取值范围是( )
A.[0, ) ) | B. | C. | D. |
17.在 中,
中, 分别为内角
分别为内角 的对边,且
的对边,且

(Ⅰ)求 的大小;
的大小;
(Ⅱ)若 ,是判断
,是判断 的形状。
的形状。
 中,
中, 分别为内角
分别为内角 的对边,且
的对边,且
(Ⅰ)求
 的大小;
的大小;(Ⅱ)若
 ,是判断
,是判断 的形状。
的形状。18.为了比较注射A,B两种药物后产生的皮肤疱疹的面积,选200只家兔做实验,将这200只家兔随即地分成两组。每组100只,其中一组注射药物A,另一组注射药物B。下表1和表2分别是注射药物A和药物B后的实验结果。(疱疹面积单位: )
)

(Ⅰ)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小;

(Ⅱ)完成下面 列联表,并回答能否有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”。.C#
列联表,并回答能否有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”。.C#

附:

 )
)
(Ⅰ)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小;

(Ⅱ)完成下面
 列联表,并回答能否有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”。.C#
列联表,并回答能否有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”。.C#
附:


19.设 ,
, 分别为椭圆
分别为椭圆
 的左右焦点,过
的左右焦点,过 的直线
的直线 与椭圆
与椭圆 相交于
相交于 ,
, 两点,直线
两点,直线 的倾斜角为
的倾斜角为 ,
, 到直线
到直线 的距离为
的距离为 。
。
(Ⅰ)求椭圆 的焦距;
的焦距;
(Ⅱ)如果 ,求椭圆
,求椭圆 的方程。
的方程。
 ,
, 分别为椭圆
分别为椭圆
 的左右焦点,过
的左右焦点,过 的直线
的直线 与椭圆
与椭圆 相交于
相交于 ,
, 两点,直线
两点,直线 的倾斜角为
的倾斜角为 ,
, 到直线
到直线 的距离为
的距离为 。
。(Ⅰ)求椭圆
 的焦距;
的焦距;(Ⅱ)如果
 ,求椭圆
,求椭圆 的方程。
的方程。20.已知函数 .
.
(Ⅰ)讨论函数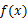 的单调性;
的单调性;
(Ⅱ)设 ,证明:对任意
,证明:对任意 ,
, 。
。
 .
.(Ⅰ)讨论函数
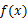 的单调性;
的单调性;(Ⅱ)设
 ,证明:对任意
,证明:对任意 ,
, 。
。21.已知 为半圆
为半圆 (
( 为参数,
为参数, )上的点,点
)上的点,点 的坐标为
的坐标为 ,
, 为坐标原点,点
为坐标原点,点 在射线
在射线 上,线段
上,线段 与
与 的弧
的弧 的长度均为
的长度均为 。
。
(Ⅰ)以 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,求点
轴的正半轴为极轴建立极坐标系,求点 的坐标;
的坐标;
(Ⅱ)求直线 的参数方程
的参数方程
 为半圆
为半圆 (
( 为参数,
为参数, )上的点,点
)上的点,点 的坐标为
的坐标为 ,
, 为坐标原点,点
为坐标原点,点 在射线
在射线 上,线段
上,线段 与
与 的弧
的弧 的长度均为
的长度均为 。
。(Ⅰ)以
 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,求点
轴的正半轴为极轴建立极坐标系,求点 的坐标;
的坐标;(Ⅱ)求直线
 的参数方程
的参数方程
22. 已知 均为正数,证明:
均为正数,证明: ,并确定
,并确定 为何值时,等号成立.
为何值时,等号成立.
 均为正数,证明:
均为正数,证明: ,并确定
,并确定 为何值时,等号成立.
为何值时,等号成立.23.如图,棱柱 的侧面
的侧面 是菱形,
是菱形,

(Ⅰ)证明:平面
 平面
平面 ;
;
(Ⅱ)设 是
是 上的点,且
上的点,且 平面
平面 ,求
,求 的值.
的值.
 的侧面
的侧面 是菱形,
是菱形,

(Ⅰ)证明:平面

 平面
平面 ;
;(Ⅱ)设
 是
是 上的点,且
上的点,且 平面
平面 ,求
,求 的值.
的值.
24.如图,△ABC的角平分线AD的延长线交它的外接圆于点
(Ⅰ)证明:△ABE∽△ADC;
(Ⅱ)若△ABC的面积 ,求
,求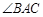 的大小.
的大小.

(Ⅰ)证明:△ABE∽△ADC;
(Ⅱ)若△ABC的面积
 ,求
,求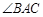 的大小.
的大小.
 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
