全一卷
1.设函数 的定义域
的定义域 ,函数y=ln(1-x)的定义域为
,函数y=ln(1-x)的定义域为 ,则
,则
 的定义域
的定义域 ,函数y=ln(1-x)的定义域为
,函数y=ln(1-x)的定义域为 ,则
,则
| A.(1,2) | B.(1,2] | C.(-2,1) | D.[-2,1) |
2.已知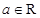 ,
, 是虚数单位,若
是虚数单位,若 ,
, ,则
,则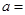 ( )
( )
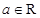 ,
, 是虚数单位,若
是虚数单位,若 ,
, ,则
,则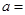 ( )
( )A.1或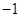 | B.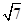 或 或 | C. | D. |
3.已知命题p: ;命题q:若a>b,则a2>b2,下列命题为真命题的是
;命题q:若a>b,则a2>b2,下列命题为真命题的是
 ;命题q:若a>b,则a2>b2,下列命题为真命题的是
;命题q:若a>b,则a2>b2,下列命题为真命题的是A. | B. | C. | D. |
4.为了研究某班学生的脚长 (单位厘米)和身高
(单位厘米)和身高 (单位厘米)的关系,从该班随机抽取
(单位厘米)的关系,从该班随机抽取 名学生,根据测量数据的散点图可以看出
名学生,根据测量数据的散点图可以看出 与
与 之间有线性相关关系,设其回归直线方程为
之间有线性相关关系,设其回归直线方程为 .已知
.已知 ,
, ,
, .该班某学生的脚长为
.该班某学生的脚长为 ,据此估计其身高为
,据此估计其身高为
 (单位厘米)和身高
(单位厘米)和身高 (单位厘米)的关系,从该班随机抽取
(单位厘米)的关系,从该班随机抽取 名学生,根据测量数据的散点图可以看出
名学生,根据测量数据的散点图可以看出 与
与 之间有线性相关关系,设其回归直线方程为
之间有线性相关关系,设其回归直线方程为 .已知
.已知 ,
, ,
, .该班某学生的脚长为
.该班某学生的脚长为 ,据此估计其身高为
,据此估计其身高为A. | B. | C. | D. |
5.执行两次下图所示的程序框图,若第一次输入的x的值为7,第二次输入的x的值为9,则第一次、第二次输出的a的值分别为( )


| A.0,0 | B.1,1 |
| C.0,1 | D.1,0 |
6.若a>b>0,且ab=1,则下列不等式成立的是
A. | B.  |
C.  | D.  |
7.从分别标有1,2,…,9的9张卡片中不放回地随机抽取2次,每次抽取1张.则抽到的2张卡片上的数奇偶性不同的概率是
A. | B. | C. | D.  |
8.在 中,角
中,角 的对边分别为
的对边分别为 ,
, ,
, .若
.若 为锐角三角形,且满足
为锐角三角形,且满足 ,则下列等式成立的是
,则下列等式成立的是
 中,角
中,角 的对边分别为
的对边分别为 ,
, ,
, .若
.若 为锐角三角形,且满足
为锐角三角形,且满足 ,则下列等式成立的是
,则下列等式成立的是A. | B. | C. | D. |
9.已知当 时,函数
时,函数 的图象与
的图象与 的图象有且只有一个交点,则正实数m的取值范围是
的图象有且只有一个交点,则正实数m的取值范围是
 时,函数
时,函数 的图象与
的图象与 的图象有且只有一个交点,则正实数m的取值范围是
的图象有且只有一个交点,则正实数m的取值范围是A. | B.  |
C.  | D.  |
10.已知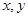 满足
满足 ,则
,则 的最大值是
的最大值是__________ .
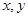 满足
满足 ,则
,则 的最大值是
的最大值是11.已知 的展开式中含有
的展开式中含有 项的系数是54,则n=
项的系数是54,则n=_____________ .
 的展开式中含有
的展开式中含有 项的系数是54,则n=
项的系数是54,则n=12.已知 ,
, 是互相垂直的单位向量,若
是互相垂直的单位向量,若 与
与 λ
λ 的夹角为60°,则实数λ的值是
的夹角为60°,则实数λ的值是__ .
 ,
, 是互相垂直的单位向量,若
是互相垂直的单位向量,若 与
与 λ
λ 的夹角为60°,则实数λ的值是
的夹角为60°,则实数λ的值是13.由一个长方体和两个 圆柱体构成的几何体的三视图如图,则该几何体的体积为___.
圆柱体构成的几何体的三视图如图,则该几何体的体积为___. 
 圆柱体构成的几何体的三视图如图,则该几何体的体积为___.
圆柱体构成的几何体的三视图如图,则该几何体的体积为___. 
14.在平面直角坐标系 中,双曲线
中,双曲线 的右支与焦点为
的右支与焦点为 的抛物线
的抛物线 交于
交于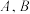 两点,若
两点,若 ,则该双曲线的渐近线方程为
,则该双曲线的渐近线方程为_________ .
 中,双曲线
中,双曲线 的右支与焦点为
的右支与焦点为 的抛物线
的抛物线 交于
交于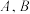 两点,若
两点,若 ,则该双曲线的渐近线方程为
,则该双曲线的渐近线方程为15.若函数
 是自然对数的底数
是自然对数的底数 在
在 的定义域上单调递增,则称函数
的定义域上单调递增,则称函数 具有M性质,下列函数中所有具有M性质的函数的序号为
具有M性质,下列函数中所有具有M性质的函数的序号为
① ②
② ③
③ ④
④

 是自然对数的底数
是自然对数的底数 在
在 的定义域上单调递增,则称函数
的定义域上单调递增,则称函数 具有M性质,下列函数中所有具有M性质的函数的序号为
具有M性质,下列函数中所有具有M性质的函数的序号为①
 ②
② ③
③ ④
④
16.设函数 ,其中
,其中 .已知
.已知 .
.
(Ⅰ)求 ;
;
(Ⅱ)将函数 的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移
的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移 个单位,得到函数
个单位,得到函数 的图象,求
的图象,求 在
在 上的最小值.
上的最小值.
 ,其中
,其中 .已知
.已知 .
.(Ⅰ)求
 ;
;(Ⅱ)将函数
 的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移
的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移 个单位,得到函数
个单位,得到函数 的图象,求
的图象,求 在
在 上的最小值.
上的最小值.17.如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是 的中点.
的中点.

(1)设P是 上的一点,且AP⊥BE,求∠CBP的大小;
上的一点,且AP⊥BE,求∠CBP的大小;
(2)当AB=3,AD=2时,求二面角E-AG-C的大小.
 的中点.
的中点.
(1)设P是
 上的一点,且AP⊥BE,求∠CBP的大小;
上的一点,且AP⊥BE,求∠CBP的大小;(2)当AB=3,AD=2时,求二面角E-AG-C的大小.
18.在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者A1,A2,A3,A4,A5,A6和4名女志愿者B1,B2,B3,B4,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.
(I)求接受甲种心理暗示的志愿者中包含A1但不包含 的频率.
的频率.
(II)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列与数学期望EX.
(I)求接受甲种心理暗示的志愿者中包含A1但不包含
 的频率.
的频率.(II)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列与数学期望EX.
19.已知 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)如图,在平面直角坐标系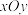 中,依次连接点
中,依次连接点 得到折线
得到折线 ,求由该折线与直线
,求由该折线与直线 ,
, 所围成的区域的面积
所围成的区域的面积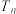 .
.
.

 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且
(Ⅰ)求数列
 的通项公式;
的通项公式;(Ⅱ)如图,在平面直角坐标系
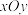 中,依次连接点
中,依次连接点 得到折线
得到折线 ,求由该折线与直线
,求由该折线与直线 ,
, 所围成的区域的面积
所围成的区域的面积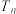 .
..

20.已知函数 ,
, ,其中
,其中 是自然对数的底数.
是自然对数的底数.
(Ⅰ)求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)令 ,讨论
,讨论 的单调性并判断有无极值,有极值时求出极值.
的单调性并判断有无极值,有极值时求出极值.
 ,
, ,其中
,其中 是自然对数的底数.
是自然对数的底数.(Ⅰ)求曲线
 在点
在点 处的切线方程;
处的切线方程;(Ⅱ)令
 ,讨论
,讨论 的单调性并判断有无极值,有极值时求出极值.
的单调性并判断有无极值,有极值时求出极值.21.在平面直角坐标系 中,椭圆
中,椭圆 :
:
 的离心率为
的离心率为 ,焦距为
,焦距为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)如图,动直线 :
: 交椭圆
交椭圆 于
于 两点,
两点, 是椭圆
是椭圆 上一点,直线
上一点,直线 的斜率为
的斜率为 ,且
,且 ,
, 是线段
是线段 延长线上一点,且
延长线上一点,且 ,
, 的半径为
的半径为 ,
, 是
是 的两条切线,切点分别为
的两条切线,切点分别为 .求
.求 的最大值,并求取得最大值时直线
的最大值,并求取得最大值时直线 的斜率.
的斜率.

 中,椭圆
中,椭圆 :
:
 的离心率为
的离心率为 ,焦距为
,焦距为 .
.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)如图,动直线
 :
: 交椭圆
交椭圆 于
于 两点,
两点, 是椭圆
是椭圆 上一点,直线
上一点,直线 的斜率为
的斜率为 ,且
,且 ,
, 是线段
是线段 延长线上一点,且
延长线上一点,且 ,
, 的半径为
的半径为 ,
, 是
是 的两条切线,切点分别为
的两条切线,切点分别为 .求
.求 的最大值,并求取得最大值时直线
的最大值,并求取得最大值时直线 的斜率.
的斜率.
 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
