全一卷
1.已知集合 ,
, ,则
,则 ()
()
 ,
, ,则
,则 ()
()A. | B. | C. | D. |
2.某几何体的三视图如图所示(单位: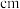 ),则该几何体的体积是
),则该几何体的体积是

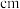 ),则该几何体的体积是
),则该几何体的体积是
A.  | B.  | C.  | D.  |
3.已知 是公差
是公差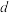 不为零的等差数列,其前
不为零的等差数列,其前 项和为
项和为 ,若
,若 成等比数列,则
成等比数列,则
 是公差
是公差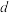 不为零的等差数列,其前
不为零的等差数列,其前 项和为
项和为 ,若
,若 成等比数列,则
成等比数列,则A. | B. |
C. | D. |
4.命题“ 且
且 的否定形式是( )
的否定形式是( )
 且
且 的否定形式是( )
的否定形式是( )A. 且 且 |
B. 或 或 |
C. 且 且 |
D. 或 或 |
5.如图,设抛物线 的焦点为
的焦点为  ,不经过焦点的直线上有三个不同的点
,不经过焦点的直线上有三个不同的点 ,
,  ,
, ,其中点
,其中点  ,
, 在抛物线上,点
在抛物线上,点  在
在 轴上,则
轴上,则  与
与 的面积之比是
的面积之比是

 的焦点为
的焦点为  ,不经过焦点的直线上有三个不同的点
,不经过焦点的直线上有三个不同的点 ,
,  ,
, ,其中点
,其中点  ,
, 在抛物线上,点
在抛物线上,点  在
在 轴上,则
轴上,则  与
与 的面积之比是
的面积之比是
A. | B. | C. | D. |
6.设 ,
, 是有限集,定义
是有限集,定义 ,其中
,其中 表示有限集A中的元素个数,命题①:对任意有限集
表示有限集A中的元素个数,命题①:对任意有限集 ,
, ,“
,“ ”是“
”是“  ”的充分必要条件;
”的充分必要条件;
命题②:对任意有限集 ,
, ,
, ,
, ,
,
 ,
, 是有限集,定义
是有限集,定义 ,其中
,其中 表示有限集A中的元素个数,命题①:对任意有限集
表示有限集A中的元素个数,命题①:对任意有限集 ,
, ,“
,“ ”是“
”是“  ”的充分必要条件;
”的充分必要条件;命题②:对任意有限集
 ,
, ,
, ,
, ,
,| A.命题①和命题②都成立 |
| B.命题①和命题②都不成立 |
| C.命题①成立,命题②不成立 |
| D.命题①不成立,命题②成立 |
7.存在函数 满足,对任意
满足,对任意 都有
都有
 满足,对任意
满足,对任意 都有
都有A. | B. |
C. | D. |
8.如图,已知 ,
, 是
是 的中点,沿直线
的中点,沿直线 将
将 折成
折成 ,所成二面角
,所成二面角 的平面角为
的平面角为 ,则
,则

 ,
, 是
是 的中点,沿直线
的中点,沿直线 将
将 折成
折成 ,所成二面角
,所成二面角 的平面角为
的平面角为 ,则
,则
A. | B. | C. | D. |
9.双曲线 的焦距是
的焦距是_____ ,渐近线方程是__________ .
 的焦距是
的焦距是10.已知函数 ,则
,则 ,
, 的最小值是 .
的最小值是 .
 ,则
,则 ,
, 的最小值是 .
的最小值是 .11.函数 的最小正周期是 ,单调递减区间是 .
的最小正周期是 ,单调递减区间是 .
 的最小正周期是 ,单调递减区间是 .
的最小正周期是 ,单调递减区间是 .12.若 ,则
,则 .
.
 ,则
,则 .
.13.如图,三棱锥 中,
中,  ,点
,点 分别是
分别是 的中点,则异面直线
的中点,则异面直线 所成的角的余弦值是
所成的角的余弦值是________ .

 中,
中,  ,点
,点 分别是
分别是 的中点,则异面直线
的中点,则异面直线 所成的角的余弦值是
所成的角的余弦值是
14.若实数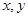 满足
满足 ,则
,则 的最小值是 .
的最小值是 .
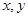 满足
满足 ,则
,则 的最小值是 .
的最小值是 .15.已知 是空间单位向量,
是空间单位向量, ,若空间向量
,若空间向量 满足
满足 ,且对于任意
,且对于任意 ,
, ,则
,则
_____ ,
_____ ,
_____ .
 是空间单位向量,
是空间单位向量, ,若空间向量
,若空间向量 满足
满足 ,且对于任意
,且对于任意 ,
, ,则
,则


16.在 中,内角
中,内角  ,
, ,
,  所对的边分别为
所对的边分别为 ,
,  ,
, ,已知
,已知  ,
, =
= 
 .
.
(1)求 的值;
的值;
(2)若 的面积为3,求
的面积为3,求  的值.
的值.
 中,内角
中,内角  ,
, ,
,  所对的边分别为
所对的边分别为 ,
,  ,
, ,已知
,已知  ,
, =
= 
 .
.(1)求
 的值;
的值;(2)若
 的面积为3,求
的面积为3,求  的值.
的值.17.如图,在三棱柱 -中,
-中,  ,
, ,
,  ,
, 在底面
在底面  的射影为
的射影为 的中点,
的中点,  为
为 的中点.
的中点.

(1)证明: D
D  平面
平面 ;
;
(2)求二面角 -BD-
-BD-  的平面角的余弦值.
的平面角的余弦值.
 -中,
-中,  ,
, ,
,  ,
, 在底面
在底面  的射影为
的射影为 的中点,
的中点,  为
为 的中点.
的中点.
(1)证明:
 D
D  平面
平面 ;
;(2)求二面角
 -BD-
-BD-  的平面角的余弦值.
的平面角的余弦值.18.(本题满分15分)已知函数 ,记
,记 是
是 在区间
在区间 上的最大值.
上的最大值.
(1)证明:当 时,
时, ;
;
(2)当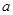 ,
, 满足
满足 ,求
,求 的最大值.
的最大值.
 ,记
,记 是
是 在区间
在区间 上的最大值.
上的最大值.(1)证明:当
 时,
时, ;
;(2)当
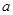 ,
, 满足
满足 ,求
,求 的最大值.
的最大值.19.已知椭圆 上两个不同的点
上两个不同的点 ,
, 关于直线
关于直线 对称.
对称.

(1)求实数 的取值范围;
的取值范围;
(2)求 面积的最大值(
面积的最大值( 为坐标原点).
为坐标原点).
 上两个不同的点
上两个不同的点 ,
, 关于直线
关于直线 对称.
对称.
(1)求实数
 的取值范围;
的取值范围;(2)求
 面积的最大值(
面积的最大值( 为坐标原点).
为坐标原点).20.已知数列 满足
满足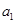 =
= 且
且 =
= -
- (
(
 ).
).
(1)证明:1 (
(
 );
);
(2)设数列 的前
的前 项和为
项和为 ,证明
,证明 (
(
 ).
).
 满足
满足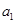 =
= 且
且 =
= -
- (
(
 ).
).(1)证明:1
 (
(
 );
);(2)设数列
 的前
的前 项和为
项和为 ,证明
,证明 (
(
 ).
). 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
