搜索
全一卷
难度系数：0.65 
答案解析
有奖纠错
1．在△ABC中，∠A、∠B、∠C的对边长分别为a、b、c.命题
，且b+c=2a；命题
为正三角形.则命题P是命题q的（）条件.
，且b+c=2a；命题
为正三角形.则命题P是命题q的（）条件.| A．充分必要 |
| B．充分但不必要 |
| C．必要但不充分 |
| D．既不充分又不必要 |
2．若复数
，则
（）
，则
（）| A．-1 | B． | C． | D．1 |
3．已知函数
，当
时，记
的最小值为m.则m的最大值为（）.
，当
时，记
的最小值为m.则m的最大值为（）.| A．-2 | B．0 | C． | D．l |
4．对任意正整数n与
，
表示不超过
（
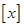表示不超过实数x的最大整数）且与n互素的正整数的个数.则
（）.
，
表示不超过
（
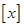表示不超过实数x的最大整数）且与n互素的正整数的个数.则
（）.| A．l1 | B．13 | C．14 | D．19 |
5．设数列
满足
，
.若
为的前n项和，则
的个位数字为（）.
满足
，
.若
为的前n项和，则
的个位数字为（）.| A．l | B．2 | C．5 | D．6 |
6．已知
、
为椭圆与双曲线的公共焦点，P为它们的一个公共点，且
.则该椭圆与双曲线的离心率之积的最小值为.
、为椭圆与双曲线的公共焦点，P为它们的一个公共点，且.则该椭圆与双曲线的离心率之积的最小值为.A． | B． | C．l | D． |
7．在
的展开式中
的系数是______ ．（用具体数作答）
的展开式中
的系数是8．若实数
、
、
构成以2为公比的等比数列，sinα、sinβ、sinγ构成等比数列，则cosa=_____.
、
、
构成以2为公比的等比数列，sinα、sinβ、sinγ构成等比数列，则cosa=_____.9．已知正四棱锥S-ABCD的侧棱长为4，
，在侧棱SB、SC、SD分别取点E、F、G则空间四边形AEFG周长的最小值为________.
，在侧棱SB、SC、SD分别取点E、F、G则空间四边形AEFG周长的最小值为________.10．已知△ABC的外心为O，且
，则
________ .
，则
11．设实数x、y、z、w满足
.则
的最大值为________.
.则
的最大值为________.12．对于任何集合S，用
表示集合S中的元素个数，用n（S）表示集合S的子集个数.若A、B、C为三个有限集，且满足（1）
；（2）
.则
的最大值为_______.
表示集合S中的元素个数，用n（S）表示集合S的子集个数.若A、B、C为三个有限集，且满足（1）
；（2）
.则
的最大值为_______.13．设等比数列的前n项和为
（r为常数）.记
.
（1）求数列
的前n项和
；
（2）若对于任意的正整数n，均有
，求实数k的最大值.
的前n项和为
（r为常数）.记
.（1）求数列
的前n项和
；（2）若对于任意的正整数n，均有
，求实数k的最大值.14．已知a、b、c为正实数.证明：
.
.15．已知拋物线
过定点C（l，2），在抛物线上任取不同于点C的一点A，直线AC与直线y=x+3交于点P，过点P作x轴的平行线，与抛物线交于点B.
（1）证明：直线AB过定点；
（2）求△ABC面积的最小值.
过定点C（l，2），在抛物线上任取不同于点C的一点A，直线AC与直线y=x+3交于点P，过点P作x轴的平行线，与抛物线交于点B.（1）证明：直线AB过定点；
（2）求△ABC面积的最小值.
16．已知a为实数，函数
.请讨论函数单调性.
.请讨论函数单调性.