全一卷
1.设集合 ,则
,则
 ,则
,则
A. | B. | C. | D. |
2. ( )
( )
 ( )
( )A. | B. |
C. | D. |
3.函数 的最小正周期为
的最小正周期为
 的最小正周期为
的最小正周期为A. | B. | C. | D. |
4.设非零向量 ,
, 满足
满足 ,则
,则
 ,
, 满足
满足 ,则
,则A. ⊥ ⊥ | B. |
C. ∥ ∥ | D. |
5.若 ,则双曲线
,则双曲线 的离心率的取值范围是
的离心率的取值范围是
 ,则双曲线
,则双曲线 的离心率的取值范围是
的离心率的取值范围是A. | B. | C. | D. |
6.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为


A. | B. | C. | D. |
7.设x,y满足约束条件 则z=2x+y的最小值是( )
则z=2x+y的最小值是( )
 则z=2x+y的最小值是( )
则z=2x+y的最小值是( )| A.-15 | B.-9 | C.1 | D.9 |
8.函数 的单调递增区间是
的单调递增区间是
 的单调递增区间是
的单调递增区间是A. | B. |
C. | D. |
9.甲、乙、丙,丁四位同学一起去问老师询问成语竞赛的成绩。老师说:你们四人中有两位优秀,两位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩,根据以上信息,则( )
| A.乙、丁可以知道自己的成绩 | B.乙可以知道四人的成绩 |
| C.乙、丁可以知道对方的成绩 | D.丁可以知道四人的成绩 |
10.执行如图所示的程序框图,如果输入的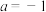 ,则输出的
,则输出的

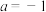 ,则输出的
,则输出的

| A.2 | B.3 | C.4 | D.5 |
11.从分别写有 的
的 张卡片中随机抽取
张卡片中随机抽取 张,放回后再随机抽取
张,放回后再随机抽取 张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为
张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为
 的
的 张卡片中随机抽取
张卡片中随机抽取 张,放回后再随机抽取
张,放回后再随机抽取 张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为
张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为A. | B. | C. | D. |
12.过抛物线C:y2=4x的焦点F,且斜率为 的直线交C于点M(M在x轴的上方),l为C的准线,点N在l上且MN⊥l,则M到直线NF的距离为( )
的直线交C于点M(M在x轴的上方),l为C的准线,点N在l上且MN⊥l,则M到直线NF的距离为( )
 的直线交C于点M(M在x轴的上方),l为C的准线,点N在l上且MN⊥l,则M到直线NF的距离为( )
的直线交C于点M(M在x轴的上方),l为C的准线,点N在l上且MN⊥l,则M到直线NF的距离为( )A. | B. | C. | D. |
13.函数 的最大值为
的最大值为__________ .
 的最大值为
的最大值为14.已知函数 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, ,则
,则
__________ .
 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, ,则
,则
15.长方体的长,宽,高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为__________ .
16. 的内角
的内角 的对边分别为
的对边分别为 ,若
,若 ,则
,则
________ .
 的内角
的内角 的对边分别为
的对边分别为 ,若
,若 ,则
,则
17.已知等差数列 的前
的前 项和为
项和为 ,等比数列
,等比数列 的前
的前 项和为
项和为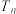 ,且
,且 ,
, ,
, .
.
(1)若 ,求
,求 的通项公式;
的通项公式;
(2)若 ,求
,求 .
.
 的前
的前 项和为
项和为 ,等比数列
,等比数列 的前
的前 项和为
项和为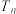 ,且
,且 ,
, ,
, .
.(1)若
 ,求
,求 的通项公式;
的通项公式;(2)若
 ,求
,求 .
.18.四棱锥 中,侧面
中,侧面 为等边三角形且垂直于底面
为等边三角形且垂直于底面 ,
,
(1)证明:直线 平面
平面 ;
;
(2)若△ 面积为
面积为 ,求四棱锥
,求四棱锥 的体积.
的体积.

 中,侧面
中,侧面 为等边三角形且垂直于底面
为等边三角形且垂直于底面 ,
,
(1)证明:直线
 平面
平面 ;
;(2)若△
 面积为
面积为 ,求四棱锥
,求四棱锥 的体积.
的体积.
19.海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg), 其频率分布直方图如下:
(1)记A表示事件“旧养殖法的箱产量低于50kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:



(1)记A表示事件“旧养殖法的箱产量低于50kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
| 箱产量<50kg | 箱产量≥50kg | |
| 旧养殖法 | ||
| 新养殖法 |
(3)根据箱产量的频率分布直方图,对两种养殖方法的优劣进行较.
附:
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |


20.设O为坐标原点,动点M在椭圆C 上,过M作x轴的垂线,垂足为N,点P满足
上,过M作x轴的垂线,垂足为N,点P满足 .
.
(1)求点P的轨迹方程;
(2)设点 在直线
在直线 上,且
上,且 .证明:过点P且垂直于OQ的直线
.证明:过点P且垂直于OQ的直线 过C的左焦点F.
过C的左焦点F.
 上,过M作x轴的垂线,垂足为N,点P满足
上,过M作x轴的垂线,垂足为N,点P满足 .
.(1)求点P的轨迹方程;
(2)设点
 在直线
在直线 上,且
上,且 .证明:过点P且垂直于OQ的直线
.证明:过点P且垂直于OQ的直线 过C的左焦点F.
过C的左焦点F.21.设函数 .
.
(I)讨论函数 的单调性;
的单调性;
(II)当 时,
时, ,求实数
,求实数 的取值范围.
的取值范围.
 .
.(I)讨论函数
 的单调性;
的单调性;(II)当
 时,
时, ,求实数
,求实数 的取值范围.
的取值范围.22.在直角坐标系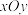 中,以坐标原点为极点,
中,以坐标原点为极点, 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线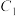 的极坐标方程为
的极坐标方程为 .
.
(1) 为曲线
为曲线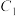 上的动点,点
上的动点,点 在线段
在线段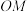 上,且满足
上,且满足 ,求点
,求点 的轨迹
的轨迹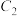 的直角坐标方程;
的直角坐标方程;
(2)设点 的极坐标为
的极坐标为 ,点
,点 在曲线
在曲线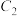 上,求
上,求 面积的最大值.
面积的最大值.
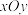 中,以坐标原点为极点,
中,以坐标原点为极点, 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线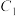 的极坐标方程为
的极坐标方程为 .
.(1)
 为曲线
为曲线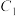 上的动点,点
上的动点,点 在线段
在线段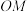 上,且满足
上,且满足 ,求点
,求点 的轨迹
的轨迹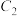 的直角坐标方程;
的直角坐标方程;(2)设点
 的极坐标为
的极坐标为 ,点
,点 在曲线
在曲线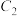 上,求
上,求 面积的最大值.
面积的最大值.23.已知 ,
, ,
, ,证明:
,证明:
(1) ;
;
(2) .
.
 ,
, ,
, ,证明:
,证明:(1)
 ;
;(2)
 .
. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
