全一卷
1.集合 ,
, ,若
,若 ,则
,则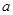 的值为( ).
的值为( ).
 ,
, ,若
,若 ,则
,则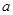 的值为( ).
的值为( ).A. | B.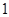 | C. | D.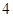 |
2.复数 等于( )
等于( )
 等于( )
等于( )A. | B. | C. | D. |
3.已知α,β表示两个不同的平面,m为平面α内的一条直线,则“ ⊥
⊥ ”是“
”是“ ⊥
⊥ ”的
”的
 ⊥
⊥ ”是“
”是“ ⊥
⊥ ”的
”的| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
4.函数 的图像大致为( )
的图像大致为( )
 的图像大致为( )
的图像大致为( )A. | B. | C. | D. |
5.
(2009山东卷文)在区间 上随机取一个数x,
上随机取一个数x, 的值介于0到
的值介于0到 之间的概率为( ).
之间的概率为( ).
(2009山东卷文)在区间
 上随机取一个数x,
上随机取一个数x, 的值介于0到
的值介于0到 之间的概率为( ).
之间的概率为( ).A. | B. | C. | D.   |
6.已知定义在 上的奇函数
上的奇函数 满足
满足 ,且在区间
,且在区间 上是增函数,则
上是增函数,则
 上的奇函数
上的奇函数 满足
满足 ,且在区间
,且在区间 上是增函数,则
上是增函数,则A. | B. |
C. | D. |
7.将函数 的图象向左平移
的图象向左平移 个单位, 再向上平移1个单位,所得图象的函数解析式是()
个单位, 再向上平移1个单位,所得图象的函数解析式是()
 的图象向左平移
的图象向左平移 个单位, 再向上平移1个单位,所得图象的函数解析式是()
个单位, 再向上平移1个单位,所得图象的函数解析式是()A. | B. | C. | D. |
8.在R上定义运算⊙: ⊙
⊙ ,则满足
,则满足 ⊙
⊙ <0的实数
<0的实数 的取值范围为( )
的取值范围为( )
 ⊙
⊙ ,则满足
,则满足 ⊙
⊙ <0的实数
<0的实数 的取值范围为( )
的取值范围为( )| A.(0,2) | B.(-2,1) | C. | D.(-1,2) |
9.定义在R上的函数f(x)满足f(x)= ,则f(3)的值为( )
,则f(3)的值为( )
 ,则f(3)的值为( )
,则f(3)的值为( )| A.-1 | B.-2 | C.1 | D.2 |
10.设P是△ABC所在平面内的一点, ,则( )
,则( )
 ,则( )
,则( )A. | B. | C. | D. |
11.若函数f(x)= (
( 且
且 )有两个零点,则实数
)有两个零点,则实数 的取值范围是 .
的取值范围是 .
 (
( 且
且 )有两个零点,则实数
)有两个零点,则实数 的取值范围是 .
的取值范围是 .12.某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元,现该公司至少要生产A类产品50件,B类产品140件,所需租赁费最少为__________元.
13.(2009山东卷理)执行右边的程序框图,输出的T= .

14.在等差数列 中,
中, ,则
,则 .
.
 中,
中, ,则
,则 .
.15.设函数 在
在 处取最小值.
处取最小值.
(Ⅰ)求 的值;(Ⅱ)在
的值;(Ⅱ)在 ABC中,
ABC中, 分别是角A,B,C的对边,已知
分别是角A,B,C的对边,已知
 ,求角C.
,求角C.
 在
在 处取最小值.
处取最小值.(Ⅰ)求
 的值;(Ⅱ)在
的值;(Ⅱ)在 ABC中,
ABC中, 分别是角A,B,C的对边,已知
分别是角A,B,C的对边,已知
 ,求角C.
,求角C.16.设 ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量 ,向量
,向量 ,
, ,动点
,动点 的轨迹为E.
的轨迹为E.
(1)求轨迹E的方程,并说明该方程所表示曲线的形状;
(2)已知 ,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且
,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且 (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程;
(3)已知 ,设直线
,设直线 与圆C:
与圆C: (1<R<2)相切于A1,且
(1<R<2)相切于A1,且 与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
 ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量 ,向量
,向量 ,
, ,动点
,动点 的轨迹为E.
的轨迹为E.(1)求轨迹E的方程,并说明该方程所表示曲线的形状;
(2)已知
 ,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且
,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且 (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程;(3)已知
 ,设直线
,设直线 与圆C:
与圆C: (1<R<2)相切于A1,且
(1<R<2)相切于A1,且 与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.17.一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1)求z的值.
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2.把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
| 轿车A | 轿车B | 轿车C | |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
(1)求z的值.
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2.把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
18.如图,在直四棱柱ABCD-A B
B C
C D
D 中,底面ABCD为等腰梯形,AB//CD,AB=4,BC=CD=2,AA
中,底面ABCD为等腰梯形,AB//CD,AB=4,BC=CD=2,AA =2, E、E
=2, E、E 分别是棱AD、AA
分别是棱AD、AA 的中点.
的中点.

(1)设F是棱AB的中点,证明:直线EE //平面FCC
//平面FCC ;
;
(2)证明:平面D1AC⊥平面BB1C1C.
 B
B C
C D
D 中,底面ABCD为等腰梯形,AB//CD,AB=4,BC=CD=2,AA
中,底面ABCD为等腰梯形,AB//CD,AB=4,BC=CD=2,AA =2, E、E
=2, E、E 分别是棱AD、AA
分别是棱AD、AA 的中点.
的中点.
(1)设F是棱AB的中点,证明:直线EE
 //平面FCC
//平面FCC ;
;(2)证明:平面D1AC⊥平面BB1C1C.
19.等比数列{ }的前n项和为
}的前n项和为 ,已知对任意的
,已知对任意的 ,点
,点 ,均在函数
,均在函数 且
且 均为常数)的图像上.
均为常数)的图像上.
(1)求r的值;
(11)当b=2时,记 ,求数列
,求数列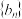 的前
的前 项和
项和 .
.
 }的前n项和为
}的前n项和为 ,已知对任意的
,已知对任意的 ,点
,点 ,均在函数
,均在函数 且
且 均为常数)的图像上.
均为常数)的图像上.(1)求r的值;
(11)当b=2时,记
 ,求数列
,求数列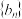 的前
的前 项和
项和 .
.20.
已知函数 ,其中
,其中 .
.
(1)当 满足什么条件时,
满足什么条件时,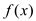 取得极值?
取得极值?
(2)已知 ,且
,且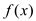 在区间
在区间 上单调递增,试用
上单调递增,试用 表示出
表示出 的取值范围.
的取值范围.
已知函数
 ,其中
,其中 .
.(1)当
 满足什么条件时,
满足什么条件时,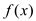 取得极值?
取得极值?(2)已知
 ,且
,且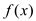 在区间
在区间 上单调递增,试用
上单调递增,试用 表示出
表示出 的取值范围.
的取值范围. 搜索
搜索
 难度系数:0.64
难度系数:0.64  答案解析
答案解析
 有奖纠错
有奖纠错
