全一卷
1.若将函数 的图像向右平移
的图像向右平移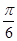 个单位长度后,与函数
个单位长度后,与函数 的图像重合,则
的图像重合,则 的最小值为
的最小值为
 的图像向右平移
的图像向右平移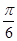 个单位长度后,与函数
个单位长度后,与函数 的图像重合,则
的图像重合,则 的最小值为
的最小值为A. | B. | C. | D. |
2.已知直线 与抛物线
与抛物线 相交于A、B两点,F为C的焦点,若
相交于A、B两点,F为C的焦点,若 ,则k=
,则k=
 与抛物线
与抛物线 相交于A、B两点,F为C的焦点,若
相交于A、B两点,F为C的焦点,若 ,则k=
,则k=A. | B. | C. | D. |
3.已知正四棱柱 中,
中, ,E为
,E为 中点,则异面直线BE与
中点,则异面直线BE与 所成角的余弦值为( )
所成角的余弦值为( )
 中,
中, ,E为
,E为 中点,则异面直线BE与
中点,则异面直线BE与 所成角的余弦值为( )
所成角的余弦值为( )A. | B. | C. | D. |
4.已知全集U={1,2,3,4,5,6,7,8},M ={1,3,5,7},N ={5,6,7},则Cu( M N)=
N)=
 N)=
N)=| A.{5,7} | B.{2,4} | C.{2.4.8} | D.{1,3,5,6,7} |
5.函数y= (x
(x 0)的反函数是
0)的反函数是
 (x
(x 0)的反函数是
0)的反函数是A. (x (x 0) 0) | B. (x (x 0) 0) |
C. (x (x 0) 0) | D. (x (x 0) 0) |
6.函数 的图像
的图像
 的图像
的图像| A.关于原点对称 | B.关于主线 对称 对称 |
C.关于 轴对称 轴对称 | D.关于直线 对称 对称 |
7.已知 ABC中,cotA=
ABC中,cotA= ,则cosA=( )
,则cosA=( )
 ABC中,cotA=
ABC中,cotA= ,则cosA=( )
,则cosA=( )A. | B. | C. | D. |
8.已知向量 ,
, ,
, ,则
,则
 ,
, ,
, ,则
,则
A. | B. | C.5 | D.25 |
9.设 则
则
 则
则A. | B. |
C. | D. |
10.双曲线 的渐近线与圆
的渐近线与圆 相切,则
相切,则 ()
()
 的渐近线与圆
的渐近线与圆 相切,则
相切,则 ()
()A. | B.2 | C.3 | D.6 |
11.甲、乙两人从4门课程中各选修2门,则甲、乙所选的课程中恰有1门相同的选法有
| A.6种 | B.12种 | C.24种 | D.30种 |
12..现在沿该正方体的一些棱将正方体剪开、外面朝上展平,得到右侧的平面图形,则标“△”的面的方位是


w.w.w..c.o.m


w.w.w..c.o.m
| A.南 | B.北 | C.西 | D.下 |
13. 的展开式中
的展开式中 的系数为 .
的系数为 .
 的展开式中
的展开式中 的系数为 .
的系数为 .14.设OA是球O的半径,M是OA的中点,过M且与OA成 角的平面截球O的表面得到圆
角的平面截球O的表面得到圆
 角的平面截球O的表面得到圆
角的平面截球O的表面得到圆A.若圆C的面积等于 ,则球O的表面积等于 . ,则球O的表面积等于 . |
15.设等比数列{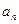 }的前n项和为
}的前n项和为 .若
.若 ,则
,则 =
=
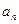 }的前n项和为
}的前n项和为 .若
.若 ,则
,则 =
= 16.已知圆O: 和点A(1,2),则过A且与圆O相切的直线与两坐标轴围成的三角形的面积等于
和点A(1,2),则过A且与圆O相切的直线与两坐标轴围成的三角形的面积等于_________
 和点A(1,2),则过A且与圆O相切的直线与两坐标轴围成的三角形的面积等于
和点A(1,2),则过A且与圆O相切的直线与两坐标轴围成的三角形的面积等于17.
已知等差数列{ }中,
}中, 求{
求{ }前n项和
}前n项和 .
.
已知等差数列{
 }中,
}中, 求{
求{ }前n项和
}前n项和 .
.18.(本小题满分12分)
设△ABC的内角A、B、C的对边长分别为a、b、c, ,
, ,求B.
,求B.
设△ABC的内角A、B、C的对边长分别为a、b、c,
 ,
, ,求B.
,求B.19.
某车间甲组有10名工人,其中有4名女工人;乙组有10名工人,其中有6名女工人.现采用分层抽样(层内采用不放回简单随即抽样)从甲、乙两组中共抽取4名工人进行技术考核.
(Ⅰ)求从甲、乙两组各抽取的人数;
(Ⅱ)求从甲组抽取的工人中恰有1名女工人的概率;
(Ⅲ)求抽取的4名工人中恰有2名男工人的概率.
某车间甲组有10名工人,其中有4名女工人;乙组有10名工人,其中有6名女工人.现采用分层抽样(层内采用不放回简单随即抽样)从甲、乙两组中共抽取4名工人进行技术考核.
(Ⅰ)求从甲、乙两组各抽取的人数;
(Ⅱ)求从甲组抽取的工人中恰有1名女工人的概率;
(Ⅲ)求抽取的4名工人中恰有2名男工人的概率.
20.设函数 ,其中常数
,其中常数
(Ⅰ)讨论 的单调性;
的单调性;
(Ⅱ)若当x≥0时, >0恒成立,求
>0恒成立,求 的取值范围.
的取值范围.
 ,其中常数
,其中常数
(Ⅰ)讨论
 的单调性;
的单调性;(Ⅱ)若当x≥0时,
 >0恒成立,求
>0恒成立,求 的取值范围.
的取值范围.21.已知椭圆C:  的离心率为
的离心率为 ,过右焦点F的直线l与C相交于A、B两点,当l的斜率为1是,坐标原点O到直线l的距离为
,过右焦点F的直线l与C相交于A、B两点,当l的斜率为1是,坐标原点O到直线l的距离为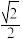 .
.
(Ⅰ)求a,b的值;
(Ⅱ)C上是否存在点P,使得当l绕F转到某一位置时,有 成立?
成立?
若存在,求出所有的P的坐标与l的方程;若不存在,说明理由.
 的离心率为
的离心率为 ,过右焦点F的直线l与C相交于A、B两点,当l的斜率为1是,坐标原点O到直线l的距离为
,过右焦点F的直线l与C相交于A、B两点,当l的斜率为1是,坐标原点O到直线l的距离为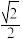 .
.(Ⅰ)求a,b的值;
(Ⅱ)C上是否存在点P,使得当l绕F转到某一位置时,有
 成立?
成立?若存在,求出所有的P的坐标与l的方程;若不存在,说明理由.
22.如图,直三棱柱ABC-A1B1C1中,AB⊥AC,D、E分别为AA1、B1C的中点,DE⊥平面BCC1.
(Ⅰ)证明:AB=AC;
(Ⅱ)设二面角A-BD-C为60°,求B1C与平面BCD所成的角的大小.
(Ⅰ)证明:AB=AC;
(Ⅱ)设二面角A-BD-C为60°,求B1C与平面BCD所成的角的大小.

 搜索
搜索
 难度系数:0.64
难度系数:0.64  答案解析
答案解析
 有奖纠错
有奖纠错
