全一卷
1.若实数 、
、 满足
满足 ,则
,则 的取值范围是_____。
的取值范围是_____。
 、
、 满足
满足 ,则
,则 的取值范围是_____。
的取值范围是_____。2.甲乙两人各自独立地抛掷一枚质地均匀的硬币,甲抛10次,乙抛11次。则乙出现正面朝上的次数比甲出现正面朝上的次数多的概率为___________。
3.在 中,
中,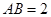 ,
, ,
, ,
, 为
为 的外心,且
的外心,且 .则
.则 =
=______________ .
 中,
中,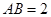 ,
, ,
, ,
, 为
为 的外心,且
的外心,且 .则
.则 =
=4.已知函数 在区间(0,2)内既有极大值又有极小值。则
在区间(0,2)内既有极大值又有极小值。则 的取值范围是______________。
的取值范围是______________。
 在区间(0,2)内既有极大值又有极小值。则
在区间(0,2)内既有极大值又有极小值。则 的取值范围是______________。
的取值范围是______________。5.集合 的元素和为奇数的非空子集的个数为_______。
的元素和为奇数的非空子集的个数为_______。
 的元素和为奇数的非空子集的个数为_______。
的元素和为奇数的非空子集的个数为_______。6.定义数列 :
: 为1+2+…+
为1+2+…+ 的末位数字,
的末位数字, 为数列
为数列 的前
的前 项之和,则
项之和,则 =______________。
=______________。
 :
: 为1+2+…+
为1+2+…+ 的末位数字,
的末位数字, 为数列
为数列 的前
的前 项之和,则
项之和,则 =______________。
=______________。7.已知双曲线 的左、右焦点分别为
的左、右焦点分别为 、
、 ,过点
,过点 作圆
作圆 的切线,与双曲线的右支交于点
的切线,与双曲线的右支交于点 ,且
,且 。则双曲线的离心率为________________。
。则双曲线的离心率为________________。
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,过点
,过点 作圆
作圆 的切线,与双曲线的右支交于点
的切线,与双曲线的右支交于点 ,且
,且 。则双曲线的离心率为________________。
。则双曲线的离心率为________________。8.过正四面体 的顶点
的顶点 作一个形状为等腰三角形的截面,且使截面与底面
作一个形状为等腰三角形的截面,且使截面与底面 所成的角为
所成的角为 。这样的截面共可作出______个。
。这样的截面共可作出______个。
 的顶点
的顶点 作一个形状为等腰三角形的截面,且使截面与底面
作一个形状为等腰三角形的截面,且使截面与底面 所成的角为
所成的角为 。这样的截面共可作出______个。
。这样的截面共可作出______个。9.已知实数 、
、 满足
满足 .试求
.试求 的取值范围。
的取值范围。
 、
、 满足
满足 .试求
.试求 的取值范围。
的取值范围。10.如图, 、
、 为
为 的切线,
的切线, 、
、 为切点,
为切点, 为线段
为线段 的中点,
的中点, 为一条割线,直线
为一条割线,直线 ∥
∥ ,
, 与
与 、
、 、
、 分别交于
分别交于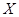 、
、 、
、 三点。证明:
三点。证明:
(1) ;
;
(2) .
.
 、
、 为
为 的切线,
的切线, 、
、 为切点,
为切点, 为线段
为线段 的中点,
的中点, 为一条割线,直线
为一条割线,直线 ∥
∥ ,
, 与
与 、
、 、
、 分别交于
分别交于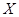 、
、 、
、 三点。证明:
三点。证明:(1)
 ;
;(2)
 .
.
11.如图,已知 、
、 为椭圆
为椭圆 ;
; 在左、右顶点,直线
在左、右顶点,直线 与椭圆
与椭圆 交于点
交于点 、
、 。设
。设 、
、 的斜率分别为
的斜率分别为 、
、 ,且
,且 :
: =1:9。
=1:9。

(1)证明:直线 过定点;
过定点;
(2)记 、
、 的面积分别为
的面积分别为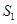 、
、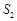 ,求
,求 的最大值。
的最大值。
 、
、 为椭圆
为椭圆 ;
; 在左、右顶点,直线
在左、右顶点,直线 与椭圆
与椭圆 交于点
交于点 、
、 。设
。设 、
、 的斜率分别为
的斜率分别为 、
、 ,且
,且 :
: =1:9。
=1:9。
(1)证明:直线
 过定点;
过定点;(2)记
 、
、 的面积分别为
的面积分别为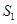 、
、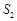 ,求
,求 的最大值。
的最大值。12.定义数列 :
: ,
, ,
, .
.
证明:(1) 为整数数列;
为整数数列;
(2) 为完全平方数。
为完全平方数。
 :
: ,
, ,
, .
.证明:(1)
 为整数数列;
为整数数列;(2)
 为完全平方数。
为完全平方数。 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
