搜索
全一卷
难度系数：0.65 
答案解析
有奖纠错
1．分解因式：
_______.
_______.2．P是圆O的直径AB的延长线上一点，PC是圆O的切线，C为切点，若PB=a，PC=a+b，则
=________ .
=3．边长为a的正方形中一点P，若△PBC为正三角形，则△PBD的面积是______.
4．a，b为正实数，方程
和
都有实根，则a+b的最小值是________.
和
都有实根，则a+b的最小值是________.5．使
位于
与
之间的正整数m=_______.
位于
与
之间的正整数m=_______.6．函数
在区间
上的最大值是______ ，最小值是________ .
在区间
上的最大值是7．已知集合
,对
，定义
为x中所有元素之和，则全体的总和S=______ .
,对
，定义
为x中所有元素之和，则全体的总和S=8．三个数：
，
，
，由小到大的排列顺序是________.
，
，
，由小到大的排列顺序是________.9．若满足方程组
的一切实数x，y，z，也满足不等式
，则实数k的取值范围是_______.
的一切实数x，y，z，也满足不等式
，则实数k的取值范围是_______.10．一个本原毕达哥拉斯三角形记为
，其中，a，b，c是三角形的三边，它们是互质的正整数，且满足
（说明：与
是全等的本原毕达哥斯拉三角形，因而认为是同一个本原毕达哥斯拉三角形）.以15为一边的本原毕达哥斯拉三角形有________个.
，其中，a，b，c是三角形的三边，它们是互质的正整数，且满足
（说明：与
是全等的本原毕达哥斯拉三角形，因而认为是同一个本原毕达哥斯拉三角形）.以15为一边的本原毕达哥斯拉三角形有________个.11．设n为自然数，若
（它表示n能被3整除），且
，则n除以15的所有可能的余数
是________.
（它表示n能被3整除），且
，则n除以15的所有可能的余数
是________.12．甲，乙，丙三人打羽毛球，每场比赛负者下，让第三人上场继续比赛，若终了统计，甲胜6场，乙胜10场，丙胜12场，则甲共比赛了_______场.
13．已知：
，
，则
________ .
，
，则
14．D为△ABC的边BC上一点，且
,若
，
，
，则
_______.
,若
，
，
，则
_______.15．在120°的二面角a-AB-β内一点P，到平面a的距离为1，到棱AB的距离为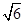
，则P到平面β的距离为________.
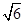，则P到平面β的距离为________.16．满足方程组
，
的正数解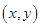
共有_______组.
，
的正数解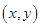
共有_______组.17．某人将连续自然数1,2,3，……逐个相加，直到某个自然数为止，由于计算时漏加了一个自然数，而得出错误的和值1989，则漏加的自然数是________.
18．方程
的所有解是________.
的所有解是________.19．
除以60的余数是______.
除以60的余数是______.20．设x，y均为正奇数，则适合
且使
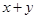不超过1989的数组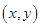有_____个.
且使
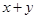不超过1989的数组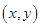有_____个.21．已知三棱锥S-ABC的底面是边长为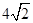
的正三角形，棱SC的长为2，且垂直于底面，D,E分别为AB,BC的中点，则异面直线CD与SE间的距离是________.
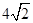的正三角形，棱SC的长为2，且垂直于底面，D,E分别为AB,BC的中点，则异面直线CD与SE间的距离是________.22．2,7,8,9,15,24,37,45,47这九个数中，相邻的若干个数之和能被17整除，则这样的数组有___ 组.
23．设a，b，c为满足不等式
的整数，且
能被abc整除，则所有可能的数组（a，b，c）是________.
的整数，且
能被abc整除，则所有可能的数组（a，b，c）是________.24．已知黄鸡、花鸡生蛋规律如下，黄鸡停产一天后连续二天每天生一个蛋，再停产一天，…，花鸡停产一天后连续四天每天生一个蛋，再停产一天，…，在第一天，二鸡都停产，从第1个星期到第20个星期内，记第n个星期黄鸡生蛋数为
，花鸡生蛋数为
，用a，b，c，d分别表示
的n个数，则
___________.
，花鸡生蛋数为
，用a，b，c，d分别表示
的n个数，则
___________.