全一卷
1.设集合 ,在集合
,在集合 上定义运算“
上定义运算“ ”:
”: ,其中,
,其中, 为
为 被4除的余数,
被4除的余数, 、
、 .则满足关系
.则满足关系 的
的 的个数为( )
的个数为( )
 ,在集合
,在集合 上定义运算“
上定义运算“ ”:
”: ,其中,
,其中, 为
为 被4除的余数,
被4除的余数, 、
、 .则满足关系
.则满足关系 的
的 的个数为( )
的个数为( )| A.1 | B.2 | C.3 | D.4 |
2.一个色子由1~6六个数字组成,根据图所示三种状态显示的数字,可推得“?”的数字为( ).


| A.6 | B.3 | C.1 | D.2 |
3.设函数 ,
,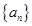 是公差为
是公差为 的等差数列,
的等差数列, .则
.则 ( )
( )
 ,
,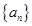 是公差为
是公差为 的等差数列,
的等差数列, .则
.则 ( )
( )| A.0 | B. | C. | D. |
4.给定平面向量(1,1).则平面向量 是将向量(1,1)经过( )变换得到的.
是将向量(1,1)经过( )变换得到的.
 是将向量(1,1)经过( )变换得到的.
是将向量(1,1)经过( )变换得到的.| A.顺时针旋转60° |
| B.顺时针旋转120° |
| C.逆时针旋转60° |
| D.逆时针旋转120° |
5.设 、
、 为非零实数,
为非零实数, 为虚数单位,
为虚数单位, .则方程
.则方程 与方程
与方程 在同一复平面内的图形(
在同一复平面内的图形( 、
、 为焦点)为( ).
为焦点)为( ).
 、
、 为非零实数,
为非零实数, 为虚数单位,
为虚数单位, .则方程
.则方程 与方程
与方程 在同一复平面内的图形(
在同一复平面内的图形( 、
、 为焦点)为( ).
为焦点)为( ).A. | B. | C. | D. |
6.在某次乒乓球单打比赛中,原计划每两名选手各比赛一场,但有三名选手各比赛两场之后就退出了,这样全部比赛只进行了50场. 则上述三名选手之间比赛的场数为( )
| A.0 | B.1 | C.2 | D.3 |
7.规定:对于 ,当且仅当
,当且仅当 时,
时, . 则
. 则 的解集为
的解集为______ .
 ,当且仅当
,当且仅当 时,
时, . 则
. 则 的解集为
的解集为8.在三棱锥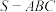 中,
中, ,
, ,
, ,
, ,
, ,
, . 则三棱锥的体积的最大值为
. 则三棱锥的体积的最大值为______ .
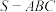 中,
中, ,
, ,
, ,
, ,
, ,
, . 则三棱锥的体积的最大值为
. 则三棱锥的体积的最大值为9.(理)一个均匀小正方体的六个面中,三个面上标以数0,两个面上标以数1,一个面上标以数2,将这个小正方体抛掷2次,则向上的数之积的数学期望是______
10.观察下列等式:
 ,
,
 ,
,
 ,
,
 ,
,
……
由以上等式推测出一般的结论:对于 ,
,
______ .
 ,
, ,
, ,
, ,
,……
由以上等式推测出一般的结论:对于
 ,
,
11.方程 的解集为
的解集为______ .
 的解集为
的解集为12.当一个非空数集 满足条件“若
满足条件“若 ,则
,则 、
、 、
、 ,且当
,且当 时,
时, ”时,称
”时,称 为一个数域. 以下四个关于数域的命题:
为一个数域. 以下四个关于数域的命题:
①0为任何数域的元素;
②若数域 有非零元素,则
有非零元素,则 ;
;
③集合 为数域;
为数域;
④有理数集为数域.
其中,真命题的编号为______(写出所有真命题的编号).
 满足条件“若
满足条件“若 ,则
,则 、
、 、
、 ,且当
,且当 时,
时, ”时,称
”时,称 为一个数域. 以下四个关于数域的命题:
为一个数域. 以下四个关于数域的命题:①0为任何数域的元素;
②若数域
 有非零元素,则
有非零元素,则 ;
;③集合
 为数域;
为数域;④有理数集为数域.
其中,真命题的编号为______(写出所有真命题的编号).
13.设椭圆 经过点
经过点 ,离心率为
,离心率为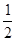 ,直线
,直线 经过椭圆
经过椭圆 的右焦点
的右焦点 ,与椭圆
,与椭圆 交于点
交于点 、
、 ,
, 、
、 、
、 在直线
在直线 上的射影依次为
上的射影依次为 、
、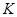 、
、 .
.
(1)求椭圆 的方程.
的方程.
(2)联结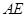 、
、 ,当直线
,当直线 的倾斜角变化时,直线
的倾斜角变化时,直线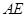 与
与 是否交于定点?若是,求出定点的坐标并给予证明;否则,说明理由.
是否交于定点?若是,求出定点的坐标并给予证明;否则,说明理由.
 经过点
经过点 ,离心率为
,离心率为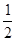 ,直线
,直线 经过椭圆
经过椭圆 的右焦点
的右焦点 ,与椭圆
,与椭圆 交于点
交于点 、
、 ,
, 、
、 、
、 在直线
在直线 上的射影依次为
上的射影依次为 、
、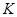 、
、 .
.(1)求椭圆
 的方程.
的方程.(2)联结
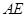 、
、 ,当直线
,当直线 的倾斜角变化时,直线
的倾斜角变化时,直线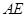 与
与 是否交于定点?若是,求出定点的坐标并给予证明;否则,说明理由.
是否交于定点?若是,求出定点的坐标并给予证明;否则,说明理由.14.在正方形 中,
中, 为边
为边 上一点(点
上一点(点 与顶点不重合). 延长
与顶点不重合). 延长 ,与
,与 的延长线交于点
的延长线交于点 . 设
. 设 、
、 、
、 的内切圆半径分别为
的内切圆半径分别为 、
、 、
、 .
.
(1)证明: ,并指出点
,并指出点 在什么位置时,等号成立;
在什么位置时,等号成立;
(2)若 ,证明:
,证明: .
.
 中,
中, 为边
为边 上一点(点
上一点(点 与顶点不重合). 延长
与顶点不重合). 延长 ,与
,与 的延长线交于点
的延长线交于点 . 设
. 设 、
、 、
、 的内切圆半径分别为
的内切圆半径分别为 、
、 、
、 .
.(1)证明:
 ,并指出点
,并指出点 在什么位置时,等号成立;
在什么位置时,等号成立;(2)若
 ,证明:
,证明: .
.15.已知函数 .
.
(1)当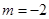 时,求函数
时,求函数 的所有零点;
的所有零点;
(2)若 有两个极值点
有两个极值点 、
、 ,证明:
,证明: .
.
 .
.(1)当
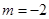 时,求函数
时,求函数 的所有零点;
的所有零点;(2)若
 有两个极值点
有两个极值点 、
、 ,证明:
,证明: .
.16.已知互异的正实数 、
、 、
、 、
、 满足
满足 .
.
证明:从 、
、 、
、 、
、 中任取三个数作为边长,共可构成四个不同的三角形.
中任取三个数作为边长,共可构成四个不同的三角形.
 、
、 、
、 、
、 满足
满足 .
.证明:从
 、
、 、
、 、
、 中任取三个数作为边长,共可构成四个不同的三角形.
中任取三个数作为边长,共可构成四个不同的三角形. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
