全一卷
1. 展开式中
展开式中 的系数为
的系数为_______________ .
 展开式中
展开式中 的系数为
的系数为2.已知直线 与圆
与圆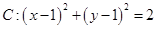 ,则
,则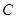 上各点到
上各点到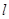 的距离的最小值为_____________。
的距离的最小值为_____________。
 与圆
与圆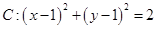 ,则
,则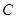 上各点到
上各点到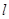 的距离的最小值为_____________。
的距离的最小值为_____________。3.从甲、乙等10名同学中挑选4名参加某校公益活动,要求甲、乙中至少有1人参加,则不同的挑选方法共有_______________ 种.
4.设数列 中,
中, ,则通项
,则通项
___________ .
 中,
中, ,则通项
,则通项
5.设集合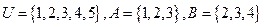 ,则
,则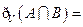 ( )
( )
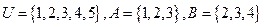 ,则
,则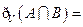 ( )
( )A. | B. | C. | D. |
6.函数 的反函数是
的反函数是
 的反函数是
的反函数是A. | B. |
C. | D. |
7.设平面向量 ,则
,则 ( )
( )
 ,则
,则 ( )
( )A. | B. | C. | D. |
8. ( )
( )
 ( )
( )A. | B. | C. | D. |
9.不等式 的解集为
的解集为
 的解集为
的解集为A. | B. | C. | D. |
10.直线 绕原点逆时针旋转
绕原点逆时针旋转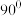 ,再向右平移1个单位,所得到的直线为(
,再向右平移1个单位,所得到的直线为(
 绕原点逆时针旋转
绕原点逆时针旋转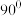 ,再向右平移1个单位,所得到的直线为(
,再向右平移1个单位,所得到的直线为(A. | B. |
C. | D. |
11.在△ABC中,角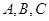 的对边分别是
的对边分别是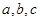 ,若
,若 ,
, ,则
,则 ( )
( )
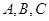 的对边分别是
的对边分别是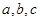 ,若
,若 ,
, ,则
,则 ( )
( )A. | B. | C. | D. |
12.设 是球心
是球心 的半径
的半径 的中点,分别过
的中点,分别过 作垂直于
作垂直于 的平面,截球面得两个圆,则这两个圆的面积比值为:
的平面,截球面得两个圆,则这两个圆的面积比值为:
 是球心
是球心 的半径
的半径 的中点,分别过
的中点,分别过 作垂直于
作垂直于 的平面,截球面得两个圆,则这两个圆的面积比值为:
的平面,截球面得两个圆,则这两个圆的面积比值为:A.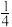 | B. | C.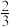 | D.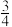 |
13.函数 满足
满足 ,若
,若 ,则
,则 ( )
( )
 满足
满足 ,若
,若 ,则
,则 ( )
( )A. | B. | C. | D. |
14.设直线 平面
平面 ,过平面
,过平面 外一点
外一点 与
与 都成
都成 角的直线有且只有:()
角的直线有且只有:()

 平面
平面 ,过平面
,过平面 外一点
外一点 与
与 都成
都成 角的直线有且只有:()
角的直线有且只有:()
| A.1条 | B.2条 | C.3条 | D.4条 |
15.已知双曲线 :
: 的左右焦点分别为
的左右焦点分别为 ,
, 为
为 的右支上一点,且
的右支上一点,且 ,则
,则 的面积等于
的面积等于
 :
: 的左右焦点分别为
的左右焦点分别为 ,
, 为
为 的右支上一点,且
的右支上一点,且 ,则
,则 的面积等于
的面积等于A. | B. | C. | D. |
16.若三棱柱的一个侧面是边长为2的正方形,另外两个侧面都是有一个内角为 的菱形,则该棱柱的体积等于
的菱形,则该棱柱的体积等于
 的菱形,则该棱柱的体积等于
的菱形,则该棱柱的体积等于 A. | B.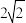 | C. | D.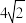 |
17.(本小题满分12分)
求函数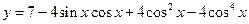 的最大值与最小值。
的最大值与最小值。
求函数
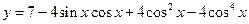 的最大值与最小值。
的最大值与最小值。18.设进入某商场的每一位顾客购买甲种商品的概率为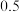 ,购买乙种商品的概率为
,购买乙种商品的概率为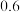 ,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.
,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.
(1)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(2)求进入商场的3位顾客中至少有2位顾客既未购买甲种也未购买乙种商品的概率.
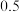 ,购买乙种商品的概率为
,购买乙种商品的概率为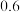 ,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.
,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.(1)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(2)求进入商场的3位顾客中至少有2位顾客既未购买甲种也未购买乙种商品的概率.
19.如图,平面 平面
平面 ,四边形
,四边形 与
与 都是直角梯形,
都是直角梯形,


 ,
,

 ,
, 分别为
分别为
 的中点.
的中点.

(Ⅰ)证明:四边形 是平行四边形;
是平行四边形;
(Ⅱ) 四点是否共面?为什么?
四点是否共面?为什么?
(Ⅲ)设 ,证明:平面
,证明:平面 平面
平面 ;
;
 平面
平面 ,四边形
,四边形 与
与 都是直角梯形,
都是直角梯形,

 ,
,

 ,
, 分别为
分别为 的中点.
的中点.
(Ⅰ)证明:四边形
 是平行四边形;
是平行四边形;(Ⅱ)
 四点是否共面?为什么?
四点是否共面?为什么?(Ⅲ)设
 ,证明:平面
,证明:平面 平面
平面 ;
;20.设 和
和 是函数
是函数 的两个极值点.
的两个极值点.
(1)求 和
和 的值;(2)求
的值;(2)求 的单调区间
的单调区间
 和
和 是函数
是函数 的两个极值点.
的两个极值点.(1)求
 和
和 的值;(2)求
的值;(2)求 的单调区间
的单调区间21.设数列 的前
的前  项和为
项和为 ,
,
(Ⅰ)求 (Ⅱ)证明:
(Ⅱ)证明:  是等比数列;(Ⅲ)求
是等比数列;(Ⅲ)求 的通项公式
的通项公式
 的前
的前  项和为
项和为 ,
,(Ⅰ)求
 (Ⅱ)证明:
(Ⅱ)证明:  是等比数列;(Ⅲ)求
是等比数列;(Ⅲ)求 的通项公式
的通项公式22.设椭圆 的左右焦点分别为
的左右焦点分别为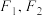 ,离心率
,离心率 ,点
,点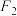 到右准线为
到右准线为 的距离为
的距离为 (Ⅰ)求
(Ⅰ)求 的值;(Ⅱ)设
的值;(Ⅱ)设 是
是 上的两个动点,
上的两个动点, ,证明:当
,证明:当 取最小值时,
取最小值时,
 的左右焦点分别为
的左右焦点分别为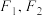 ,离心率
,离心率 ,点
,点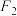 到右准线为
到右准线为 的距离为
的距离为 (Ⅰ)求
(Ⅰ)求 的值;(Ⅱ)设
的值;(Ⅱ)设 是
是 上的两个动点,
上的两个动点, ,证明:当
,证明:当 取最小值时,
取最小值时,
 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
