全一卷
1.若集合 ,
, ,则
,则
 ,
, ,则
,则
A. | B. |
C. | D. |
2.圆心为 且过原点的圆的方程是
且过原点的圆的方程是
 且过原点的圆的方程是
且过原点的圆的方程是A. |
B. |
C. |
D. |
3.下列函数中为偶函数的是
A. | B. | C. | D. |
4.某校老年、中年和青年教师的人数见下表,采用分层抽样的方法调查教师的身体状况,在抽取的样本中,青年教师有 人,则该样本的老年教师人数为( )
人,则该样本的老年教师人数为( )
 人,则该样本的老年教师人数为( )
人,则该样本的老年教师人数为( )| 类别 | 人数 |
| 老年教师 |  |
| 中年教师 |  |
| 青年教师 |  |
| 合计 |  |
A. | B. | C. | D. |
5.执行如图所示的程序框图,输出的 的值为( ).
的值为( ).

 的值为( ).
的值为( ).
A. | B.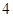 | C.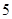 | D.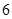 |
6.设 ,
, 是非零向量,“
是非零向量,“ ”是“
”是“ ”的
”的
 ,
, 是非零向量,“
是非零向量,“ ”是“
”是“ ”的
”的| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
7.某四棱锥的三视图如上图(右)所示,该四棱锥最长棱棱长为


| A.1 | B. | C. | D.2 |
8.某辆汽车每次加油都把油箱加满,下表记录了该车相邻两次加油时的情况.
注:“累计里程“指汽车从出厂开始累计行驶的路程
在这段时间内,该车每 千米平均耗油量为( )
千米平均耗油量为( )
| 加油时间 | 加油量(升) | 加油时的累计里程(千米) |
 年 年 月 月 日 日 |  |  |
 年 年 月 月 日 日 |  |  |
注:“累计里程“指汽车从出厂开始累计行驶的路程
在这段时间内,该车每
 千米平均耗油量为( )
千米平均耗油量为( )A. 升 升 | B. 升 升 | C. 升 升 | D. 升 升 |
9.复数 的实部为
的实部为_________ .
 的实部为
的实部为10. ,
, ,
, 三个数中最大数的是 .
三个数中最大数的是 .
 ,
, ,
, 三个数中最大数的是 .
三个数中最大数的是 .11.在 中,
中, ,
, ,
, ,则
,则
_________ .
 中,
中, ,
, ,
, ,则
,则
12.已知 是双曲线
是双曲线 (
( )的一个焦点,则
)的一个焦点,则
______ .
 是双曲线
是双曲线 (
( )的一个焦点,则
)的一个焦点,则
13.如图, 及其内部的点组成的集合记为
及其内部的点组成的集合记为 ,
, 为
为 中任意一点,则
中任意一点,则 的最大值为
的最大值为_______ .

 及其内部的点组成的集合记为
及其内部的点组成的集合记为 ,
, 为
为 中任意一点,则
中任意一点,则 的最大值为
的最大值为
14.

高三年级267位学生参加期末考试,某班37位学生的语文成绩、数学成绩与总成绩在全年级中的排名情况如下图所示,甲、乙、丙为该班的3位学生.

从这次考试成绩看,
①在甲、乙两人中,其语文成绩名次比其总成绩名次靠前的学生是
②在语文和数学两个科目中,丙同学的成绩名次更靠前的科目是
15.已知函数 .
.
(1)求 的最小正周期.
的最小正周期.
(2)求 在区间
在区间 上的最小值.
上的最小值.
 .
.(1)求
 的最小正周期.
的最小正周期.(2)求
 在区间
在区间 上的最小值.
上的最小值.16.已知等差数列 满足
满足 ,
, .
.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)设等比数列 满足
满足 ,
, ,问:
,问: 与数列
与数列 的第几项相等?
的第几项相等?
 满足
满足 ,
, .
.(Ⅰ)求
 的通项公式;
的通项公式;(Ⅱ)设等比数列
 满足
满足 ,
, ,问:
,问: 与数列
与数列 的第几项相等?
的第几项相等?17.某超市随机选取 位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
(Ⅰ)估计顾客同时购买乙和丙的概率;
(Ⅱ)估计顾客在甲、乙、丙、丁中同时购买 种商品的概率;
种商品的概率;
(Ⅲ)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中那种商品的可能性最大?
 位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买. | 甲 | 乙 | 丙 | 丁 |
 | √ | × | √ | √ |
 | × | √ | × | √ |
 | √ | √ | √ | × |
 | √ | × | √ | × |
 | √ | × | × | × |
 | × | √ | × | × |
(Ⅰ)估计顾客同时购买乙和丙的概率;
(Ⅱ)估计顾客在甲、乙、丙、丁中同时购买
 种商品的概率;
种商品的概率;(Ⅲ)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中那种商品的可能性最大?
18.如图,在三棱锥 中,平面
中,平面 平面
平面 ,
, 为等边三角形,
为等边三角形, 且
且 ,
, ,
, 分别为
分别为 ,
, 的中点.
的中点.

(1)求证: 平面
平面 ;
;
(2)求证:平面 平面
平面 ;
;
(3)求三棱锥 的体积.
的体积.
 中,平面
中,平面 平面
平面 ,
, 为等边三角形,
为等边三角形, 且
且 ,
, ,
, 分别为
分别为 ,
, 的中点.
的中点.
(1)求证:
 平面
平面 ;
;(2)求证:平面
 平面
平面 ;
; (3)求三棱锥
 的体积.
的体积.19.设函数 ,
,  .
.
(1)求 的单调区间和极值;
的单调区间和极值;
(2)证明:若 存在零点,则
存在零点,则 在区间
在区间 上仅有一个零点.
上仅有一个零点.
 ,
,  .
.(1)求
 的单调区间和极值;
的单调区间和极值;(2)证明:若
 存在零点,则
存在零点,则 在区间
在区间 上仅有一个零点.
上仅有一个零点.20.已知椭圆
 ,过点
,过点 且不过点
且不过点 的直线与椭圆
的直线与椭圆 交于
交于 ,
, 两点,直线
两点,直线 与直线
与直线 交于点
交于点 .
.
(Ⅰ)求椭圆 的离心率;
的离心率;
(Ⅱ)若 垂直于
垂直于 轴,求直线
轴,求直线 的斜率;
的斜率;
(Ⅲ)试判断直线 与直线
与直线 的位置关系,并说明理由.
的位置关系,并说明理由.

 ,过点
,过点 且不过点
且不过点 的直线与椭圆
的直线与椭圆 交于
交于 ,
, 两点,直线
两点,直线 与直线
与直线 交于点
交于点 .
.(Ⅰ)求椭圆
 的离心率;
的离心率;(Ⅱ)若
 垂直于
垂直于 轴,求直线
轴,求直线 的斜率;
的斜率;(Ⅲ)试判断直线
 与直线
与直线 的位置关系,并说明理由.
的位置关系,并说明理由. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
