搜索
全一卷
难度系数：0.85 
答案解析
有奖纠错
1．已知集合
，那么
，那么| A．（-1,2） | B．（0，1） | C．（-1,0） | D．（1,2） |
2．椭圆
的离心率是（ ）
的离心率是（ ）A． | B． | C． | D． |
3．某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：
）是
）是
A． | B． | C． | D． |
4．
若x,y满足约束条件
的取值范围是
| A．[0,6] | B．[0,4] | C．[6,  | D．[4, |
5．若函数
在区间[0,1]上的最大值是M,最小值是m,则
的值
在区间[0,1]上的最大值是M,最小值是m,则的值| A．与a有关，且与b有关 | B．与a有关，但与b无关 |
| C．与a无关，且与b无关 | D．与a无关，但与b有关 |
6．
已知等差数列
的公差为d,前n项和为
,则“d>0”是
| A．充分不必要条件 | B．必要不充分条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
7．
函数
的图象如图所示，则函数
的图象可能是
A． | B． |
C． | D． |
8．已知随机变量
满足P（=1）=pi，P（=0）=1—pi，i=1，2.若0<p1<p2<
，则
满足P（=1）=pi，P（=0）=1—pi，i=1，2.若0<p1<p2<
，则A． < ， < | B．<，> |
| C．>，< | D．>，> |
9．如图，已知正四面体D–ABC（所有棱长均相等的三棱锥），P，Q，R分别为AB，BC，CA上的点，AP=PB，
，分别记二面角D–PR–Q，D–PQ–R，D–QR–P的平面角为α,β,γ，则
，分别记二面角D–PR–Q，D–PQ–R，D–QR–P的平面角为α,β,γ，则
| A．γ<α<β | B．α<γ<β | C．α<β<γ | D．β<γ<α |
10．如图，已知平面四边形ABCD，AB⊥BC，AB＝BC＝AD＝2，CD＝3，AC与BD交于点O，记
，
，
，则
，，，则 | A．I１<I２<I３ | B．I１<I３<I２ | C．I３< I１<I２ | D．I２<I１<I３ |
11．我国古代数学家刘徽创立的“割圆术”可以估算圆周率π，理论上能把π的值计算到任意精度．祖冲之继承并发展了“割圆术”，将π的值精确到小数点后七位，其结果领先世界一千多年，“割圆术”的第一步是计算单位圆内接正六边形的面积
，
________ ．
，12．从6男2女共8名学生中选出队长1人，副队长1人，普通队员2人，组成4人服务队，要求服务队中至少有1名女生，共有__________ 种不同的选法．（用数字作答）
13．已知
，函数
在区间[1,4]上的最大值是5，则a的取值范围是__________
，函数在区间[1,4]上的最大值是5，则a的取值范围是14．已知a，b∈R，
（i是虚数单位）则
______，ab=________．
（i是虚数单位）则
______，ab=________．15．已知多项式
2=
，则
=________________ ，
=________ .
2=
，则
=
=16．已知△ABC，AB=AC=4，BC=2． 点D为AB延长线上一点，BD=2，连结CD，则△BDC的面积是______ ，cos∠BDC=_______ ．
17．已知向量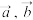
满足
，则
的最小值是___________ ，最大值是______ ．
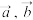满足
，则
的最小值是18．已知函数
（I）求
的值
（II）求
的最小正周期及单调递增区间.
（I）求
的值（II）求
的最小正周期及单调递增区间.19．如图，已知四棱锥P-ABCD，△PAD是以AD为斜边的等腰直角三角形，BC∥AD，CD⊥AD，PC=AD=2DC=2CB,E为PD的中点.
（I）证明：CE∥平面PAB；
（II）求直线CE与平面PBC所成角的正弦值
（I）证明：CE∥平面PAB；
（II）求直线CE与平面PBC所成角的正弦值
20．已知函数
（I）求
的导函数
（II）求在区间
上的取值范围
（I）求
的导函数（II）求
在区间
上的取值范围21．如图，已知抛物线
.点A
，抛物线上的点P（x,y）
,过点B作直线AP的垂线，垂足为Q
（I）求直线AP斜率的取值范围；
（II）求
的最大值
.点A
，抛物线上的点P（x,y）
,过点B作直线AP的垂线，垂足为Q
（I）求直线AP斜率的取值范围；
（II）求
的最大值22．已知数列
满足：
，
证明：当
时，
（I）
；
（II）
；
（III）
.
满足：
，
证明：当
时，（I）
；（II）
；（III）
.