全一卷
1.设集合 ,Z为整数集,则
,Z为整数集,则 中元素的个数是
中元素的个数是
 ,Z为整数集,则
,Z为整数集,则 中元素的个数是
中元素的个数是| A.3 | B.4 | C.5 | D.6 |
2.
设i为虚数单位,则(x+i)6的展开式中含x4的项为( )
| A.-15x4 | B.15x4 | C.-20ix4 | D.20ix4 |
3.为了得到函数 的图象,只需把函数
的图象,只需把函数 的图象上所有的点
的图象上所有的点
 的图象,只需把函数
的图象,只需把函数 的图象上所有的点
的图象上所有的点A.向左平行移动 个单位长度 个单位长度 |
B.向右平行移动 个单位长度 个单位长度 |
C.向左平行移动 个单位长度 个单位长度 |
D.向右平行移动 个单位长度 个单位长度 |
4.用数字1,2,3,4,5组成没有重复数字的五位数,其中奇数的个数为
| A.24 | B.48 |
| C.60 | D.72 |
5.某公司为激励创新,计划逐年加大研发奖金投入,若该公司 年全年投入研发奖金
年全年投入研发奖金 万元,在此基础上,每年投入的研发奖金比上一年增长
万元,在此基础上,每年投入的研发奖金比上一年增长 ,则该公司全年投入的研发奖金开始超过
,则该公司全年投入的研发奖金开始超过 万元的年份是( )(参考数据:
万元的年份是( )(参考数据: ,
, ,
, )
)
 年全年投入研发奖金
年全年投入研发奖金 万元,在此基础上,每年投入的研发奖金比上一年增长
万元,在此基础上,每年投入的研发奖金比上一年增长 ,则该公司全年投入的研发奖金开始超过
,则该公司全年投入的研发奖金开始超过 万元的年份是( )(参考数据:
万元的年份是( )(参考数据: ,
, ,
, )
)A. 年 年 | B. 年 年 | C. 年 年 | D. 年 年 |
6.秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为3,2,则输出v的值为


| A.35 | B.20 | C.18 | D.9 |
7.
设p:实数x,y满足(x-1)2+(y-1)2≤2,q:实数x,y满足 则p是q的( )
则p是q的( )
| A.必要不充分条件 |
| B.充分不必要条件 |
| C.充要条件 |
| D.既不充分也不必要条件 |
8.设 为坐标原点,
为坐标原点, 是以
是以 为焦点的抛物线
为焦点的抛物线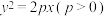 上任意一点,
上任意一点, 是线段
是线段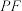 上的点,且
上的点,且 ,则直线
,则直线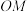 的斜率的最大值为( )
的斜率的最大值为( )

 为坐标原点,
为坐标原点, 是以
是以 为焦点的抛物线
为焦点的抛物线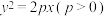 上任意一点,
上任意一点, 是线段
是线段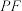 上的点,且
上的点,且 ,则直线
,则直线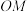 的斜率的最大值为( )
的斜率的最大值为( )
A. | B.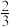 | C.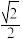 | D.1 |
9.设直线l1,l2分别是函数f(x)=  图象上点P1,P2处的切线,l1与l2垂直相交于点P,且l1,l2分别与y轴相交于点A,B,则△PAB的面积的取值范围是
图象上点P1,P2处的切线,l1与l2垂直相交于点P,且l1,l2分别与y轴相交于点A,B,则△PAB的面积的取值范围是
 图象上点P1,P2处的切线,l1与l2垂直相交于点P,且l1,l2分别与y轴相交于点A,B,则△PAB的面积的取值范围是
图象上点P1,P2处的切线,l1与l2垂直相交于点P,且l1,l2分别与y轴相交于点A,B,则△PAB的面积的取值范围是| A.(0,1) | B.(0,2) | C.(0,+∞) | D.(1,+∞) |
10.在平面内,定点A,B,C,D满足 =
= =
= ,
,
 =
=
 =
=
 =–2,动点P,M满足
=–2,动点P,M满足 =1,
=1, =
= ,则
,则 的最大值是
的最大值是
 =
= =
= ,
,
 =
=
 =
=
 =–2,动点P,M满足
=–2,动点P,M满足 =1,
=1, =
= ,则
,则 的最大值是
的最大值是A. | B. | C. | D. |
11.cos2 –sin2
–sin2 =
=________ .
 –sin2
–sin2 =
=12.同时抛掷两枚质地均匀的硬币,当至少有一枚硬币正面向上时,就说这次试验成功,则在2次试验中成功次数X的均值是 .
13.已知三棱锥的四个面都是腰长为2的等腰三角形,该三棱锥的正视图如图所示,则该三棱锥的体积是 .

14.已知函数 是定义在R上的周期为2的奇函数,当0<x<1时,
是定义在R上的周期为2的奇函数,当0<x<1时, ,则
,则
 =____________.
=____________.
 是定义在R上的周期为2的奇函数,当0<x<1时,
是定义在R上的周期为2的奇函数,当0<x<1时, ,则
,则
 =____________.
=____________.15.在平面直角坐标系中,当P(x,y)不是原点时,定义P的“伴随点”为 ;
;
当P是原点时,定义P的“伴随点”为它自身,平面曲线C上所有点的“伴随点”所构成的曲线 定义为曲线C的“伴随曲线”.现有下列命题:
定义为曲线C的“伴随曲线”.现有下列命题:
①若点A的“伴随点”是点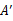 ,则点
,则点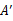 的“伴随点”是点A;
的“伴随点”是点A;
②单位圆的“伴随曲线”是它自身;
③若曲线C关于x轴对称,则其“伴随曲线” 关于y轴对称;
关于y轴对称;
④一条直线的“伴随曲线”是一条直线.
其中的真命题是_____________(写出所有真命题的序号).
 ;
;当P是原点时,定义P的“伴随点”为它自身,平面曲线C上所有点的“伴随点”所构成的曲线
 定义为曲线C的“伴随曲线”.现有下列命题:
定义为曲线C的“伴随曲线”.现有下列命题:①若点A的“伴随点”是点
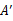 ,则点
,则点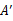 的“伴随点”是点A;
的“伴随点”是点A;②单位圆的“伴随曲线”是它自身;
③若曲线C关于x轴对称,则其“伴随曲线”
 关于y轴对称;
关于y轴对称;④一条直线的“伴随曲线”是一条直线.
其中的真命题是_____________(写出所有真命题的序号).
16.我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准 (吨)、一位居民的月用水量不超过
(吨)、一位居民的月用水量不超过 的部分按平价收费,超出
的部分按平价收费,超出 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照 ,
, 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.

(1)求直方图中 的值;
的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(3)若该市政府希望使 的居民每月的用水量不超过标准
的居民每月的用水量不超过标准 (吨),估计
(吨),估计 的值,并说明理由.
的值,并说明理由.
 (吨)、一位居民的月用水量不超过
(吨)、一位居民的月用水量不超过 的部分按平价收费,超出
的部分按平价收费,超出 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照 ,
, 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(1)求直方图中
 的值;
的值;(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(3)若该市政府希望使
 的居民每月的用水量不超过标准
的居民每月的用水量不超过标准 (吨),估计
(吨),估计 的值,并说明理由.
的值,并说明理由.17.在△ABC中,角A,B,C所对的边分别是a,b,c,且 .
.
(Ⅰ)证明: ;
;
(Ⅱ)若 ,求
,求 .
.
 .
.(Ⅰ)证明:
 ;
;(Ⅱ)若
 ,求
,求 .
.18.如图,在四棱锥P-ABCD中,AD∥BC, ADC=
ADC= PAB=90°,BC=CD=
PAB=90°,BC=CD= AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.

(I)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(II)若二面角P-CD-A的大小为45°,求直线PA与平面PCE所成角的正弦值.
 ADC=
ADC= PAB=90°,BC=CD=
PAB=90°,BC=CD= AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
(I)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(II)若二面角P-CD-A的大小为45°,求直线PA与平面PCE所成角的正弦值.
19.已知数列{ }的首项为1,
}的首项为1, 为数列{
为数列{ }的前n项和,
}的前n项和, ,其中q>0,
,其中q>0, .
.
(Ⅰ)若 成等差数列,求数列{an}的通项公式;
成等差数列,求数列{an}的通项公式;
(Ⅱ)设双曲线 的离心率为
的离心率为 ,且
,且 ,证明:
,证明: .
.
 }的首项为1,
}的首项为1, 为数列{
为数列{ }的前n项和,
}的前n项和, ,其中q>0,
,其中q>0, .
.(Ⅰ)若
 成等差数列,求数列{an}的通项公式;
成等差数列,求数列{an}的通项公式;(Ⅱ)设双曲线
 的离心率为
的离心率为 ,且
,且 ,证明:
,证明: .
.20.已知椭圆 :
: 的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线
的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线 :
: 与椭圆
与椭圆 有且只有一个公共点T.
有且只有一个公共点T.
(Ⅰ)求椭圆 的方程及点
的方程及点 的坐标;
的坐标;
(Ⅱ)设 是坐标原点,直线
是坐标原点,直线 平行于
平行于 ,与椭圆
,与椭圆 交于不同的两点
交于不同的两点 、
、 ,且与直线
,且与直线 交于点
交于点 ,证明:存在常数
,证明:存在常数 ,使得
,使得 ,并求
,并求 的值.
的值.
 :
: 的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线
的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线 :
: 与椭圆
与椭圆 有且只有一个公共点T.
有且只有一个公共点T.(Ⅰ)求椭圆
 的方程及点
的方程及点 的坐标;
的坐标;(Ⅱ)设
 是坐标原点,直线
是坐标原点,直线 平行于
平行于 ,与椭圆
,与椭圆 交于不同的两点
交于不同的两点 、
、 ,且与直线
,且与直线 交于点
交于点 ,证明:存在常数
,证明:存在常数 ,使得
,使得 ,并求
,并求 的值.
的值.21.设函数f(x)=ax2-a-lnx,其中a ∈R.
(I)讨论f(x)的单调性;
(II)确定a的所有可能取值,使得 在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数).
在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数).
(I)讨论f(x)的单调性;
(II)确定a的所有可能取值,使得
 在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数).
在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数). 搜索
搜索
 难度系数:0.64
难度系数:0.64  答案解析
答案解析
 有奖纠错
有奖纠错
