全一卷
1.设 是椭圆
是椭圆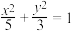 上的动点,则
上的动点,则 到该椭圆的两个焦点的距离之和为( )
到该椭圆的两个焦点的距离之和为( )
 是椭圆
是椭圆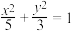 上的动点,则
上的动点,则 到该椭圆的两个焦点的距离之和为( )
到该椭圆的两个焦点的距离之和为( )A.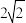 | B.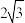 | C. | D.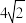 |
2.已知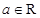 ,则“
,则“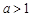 ”是“
”是“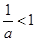 ”的( )
”的( )
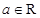 ,则“
,则“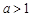 ”是“
”是“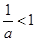 ”的( )
”的( )| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既非充分又非必要条件 |
3.《九章算术》中,称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马,设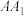 是正六棱柱的一条侧棱,如图,若阳马以该正六棱柱的顶点为顶点、以
是正六棱柱的一条侧棱,如图,若阳马以该正六棱柱的顶点为顶点、以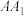 为底面矩形的一边,则这样的阳马的个数是( )
为底面矩形的一边,则这样的阳马的个数是( )

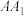 是正六棱柱的一条侧棱,如图,若阳马以该正六棱柱的顶点为顶点、以
是正六棱柱的一条侧棱,如图,若阳马以该正六棱柱的顶点为顶点、以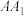 为底面矩形的一边,则这样的阳马的个数是( )
为底面矩形的一边,则这样的阳马的个数是( )
| A.4 | B.8 | C.12 | D.16 |
4.设 是含数
是含数 的有限实数集,
的有限实数集, 是定义在
是定义在 上的函数,若
上的函数,若 的图象绕原点逆时针旋转
的图象绕原点逆时针旋转 后与原图象重合,则在以下各项中,
后与原图象重合,则在以下各项中,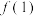 的可能取值只能是( )
的可能取值只能是( )
 是含数
是含数 的有限实数集,
的有限实数集, 是定义在
是定义在 上的函数,若
上的函数,若 的图象绕原点逆时针旋转
的图象绕原点逆时针旋转 后与原图象重合,则在以下各项中,
后与原图象重合,则在以下各项中,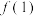 的可能取值只能是( )
的可能取值只能是( )A. | B. | C. | D. |
5.行列式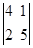 的值为___.
的值为___.
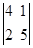 的值为___.
的值为___.6.双曲线 的渐近线方程
的渐近线方程________ .
 的渐近线方程
的渐近线方程7.在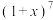 的二项展开式中,
的二项展开式中, 项的系数为 .(结果用数值表示).
项的系数为 .(结果用数值表示).
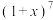 的二项展开式中,
的二项展开式中, 项的系数为 .(结果用数值表示).
项的系数为 .(结果用数值表示).8.设常数 ,函数
,函数 .若
.若 的反函数的图象经过点
的反函数的图象经过点 ,则
,则
___ .
 ,函数
,函数 .若
.若 的反函数的图象经过点
的反函数的图象经过点 ,则
,则
9.已知复数 满足
满足 (
( 是虚数单位),则
是虚数单位),则 .
.
 满足
满足 (
( 是虚数单位),则
是虚数单位),则 .
.10.记等差数列 的前
的前 项和为
项和为 ,若
,若 ,
,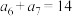 ,则
,则
____ .
 的前
的前 项和为
项和为 ,若
,若 ,
,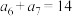 ,则
,则
11.已知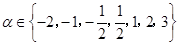 ,若幂函数
,若幂函数 为奇函数,且在
为奇函数,且在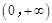 上递减,则
上递减,则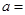
____ .
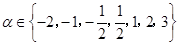 ,若幂函数
,若幂函数 为奇函数,且在
为奇函数,且在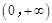 上递减,则
上递减,则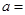
12.在平面直角坐标系中,已知点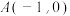 、
、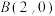 ,
, 、
、 是
是 轴上的两个动点,且
轴上的两个动点,且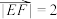 ,则的
,则的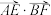 最小值为
最小值为____ .
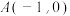 、
、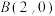 ,
, 、
、 是
是 轴上的两个动点,且
轴上的两个动点,且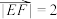 ,则的
,则的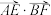 最小值为
最小值为13.有编号互不相同的五个砝码,其中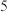 克、
克、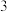 克、
克、 克砝码各一个,
克砝码各一个, 克砝码两个,从中随机选取三个,则这三个砝码的总质量为
克砝码两个,从中随机选取三个,则这三个砝码的总质量为 克的概率是
克的概率是_____ .
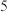 克、
克、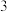 克、
克、 克砝码各一个,
克砝码各一个, 克砝码两个,从中随机选取三个,则这三个砝码的总质量为
克砝码两个,从中随机选取三个,则这三个砝码的总质量为 克的概率是
克的概率是14.设等比数列 的通项公式为
的通项公式为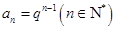 ,前
,前 项和为
项和为 .若
.若 ,则
,则 ______.
______.
 的通项公式为
的通项公式为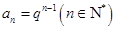 ,前
,前 项和为
项和为 .若
.若 ,则
,则 ______.
______.15.已知常数 ,函数
,函数 的图象经过点
的图象经过点 ,
, .若
.若 ,则
,则
______ .
 ,函数
,函数 的图象经过点
的图象经过点 ,
, .若
.若 ,则
,则
16.已知实数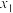 、
、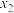 、
、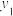 、
、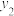 满足:
满足: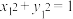 ,
,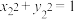 ,
,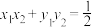 ,则
,则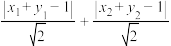 的最大值为
的最大值为______ .
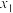 、
、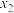 、
、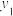 、
、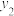 满足:
满足: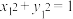 ,
,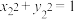 ,
,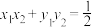 ,则
,则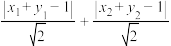 的最大值为
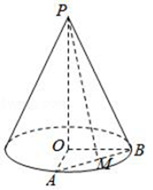
的最大值为17.已知圆锥的顶点为 ,底面圆心为
,底面圆心为 ,半径为
,半径为 .
.
(1)设圆锥的母线长为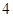 ,求圆锥的体积;
,求圆锥的体积;
(2)设 ,
,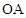 、
、 是底面半径,且
是底面半径,且 ,
, 为线段
为线段 的中点,如图.求异面直线
的中点,如图.求异面直线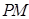 与
与 所成的角的大小.
所成的角的大小.
 ,底面圆心为
,底面圆心为 ,半径为
,半径为 .
.
(1)设圆锥的母线长为
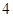 ,求圆锥的体积;
,求圆锥的体积;(2)设
 ,
,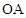 、
、 是底面半径,且
是底面半径,且 ,
, 为线段
为线段 的中点,如图.求异面直线
的中点,如图.求异面直线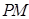 与
与 所成的角的大小.
所成的角的大小.18.设常数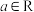 ,函数
,函数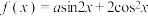 .
.
(1)若 为偶函数,求
为偶函数,求 的值;
的值;
(2)若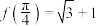 ,求方程
,求方程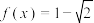 在区间
在区间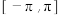 上的解.
上的解.
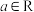 ,函数
,函数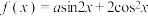 .
.(1)若
 为偶函数,求
为偶函数,求 的值;
的值;(2)若
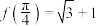 ,求方程
,求方程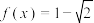 在区间
在区间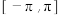 上的解.
上的解.19.某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时.某地上班族 中的成员仅以自驾或公交方式通勤.分析显示:当
中的成员仅以自驾或公交方式通勤.分析显示:当 中
中 (
( )的成员自驾时,自驾群体的人均通勤时间为
)的成员自驾时,自驾群体的人均通勤时间为 (单位:分钟),而公交群体的人均通勤时间不受
(单位:分钟),而公交群体的人均通勤时间不受 影响,恒为
影响,恒为 分钟,试根据上述分析结果回答下列问题:
分钟,试根据上述分析结果回答下列问题:
(1)当 在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
(2)求该地上班族 的人均通勤时间
的人均通勤时间 的表达式;讨论
的表达式;讨论 的单调性,并说明其实际意义.
的单调性,并说明其实际意义.
 中的成员仅以自驾或公交方式通勤.分析显示:当
中的成员仅以自驾或公交方式通勤.分析显示:当 中
中 (
( )的成员自驾时,自驾群体的人均通勤时间为
)的成员自驾时,自驾群体的人均通勤时间为 (单位:分钟),而公交群体的人均通勤时间不受
(单位:分钟),而公交群体的人均通勤时间不受 影响,恒为
影响,恒为 分钟,试根据上述分析结果回答下列问题:
分钟,试根据上述分析结果回答下列问题:(1)当
 在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?(2)求该地上班族
 的人均通勤时间
的人均通勤时间 的表达式;讨论
的表达式;讨论 的单调性,并说明其实际意义.
的单调性,并说明其实际意义.20.设常数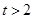 .在平面直角坐标系
.在平面直角坐标系 中,已知点
中,已知点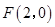 ,直线
,直线 :
: ,曲线
,曲线 :
: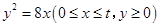 .
. 与
与 轴交于点
轴交于点 、与
、与 交于点
交于点 .
. 、
、 分别是曲线
分别是曲线 与线段
与线段 上的动点.
上的动点.
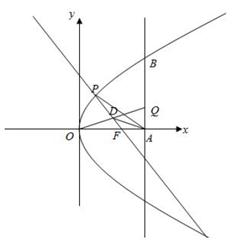
(1)用 表示点
表示点 到点
到点 距离;
距离;
(2)设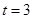 ,
,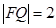 ,线段
,线段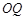 的中点在直线
的中点在直线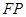 ,求
,求 的面积;
的面积;
(3)设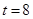 ,是否存在以
,是否存在以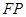 、
、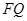 为邻边的矩形
为邻边的矩形 ,使得点
,使得点 在
在 上?若存在,求点
上?若存在,求点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
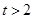 .在平面直角坐标系
.在平面直角坐标系 中,已知点
中,已知点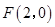 ,直线
,直线 :
: ,曲线
,曲线 :
: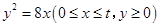 .
. 与
与 轴交于点
轴交于点 、与
、与 交于点
交于点 .
. 、
、 分别是曲线
分别是曲线 与线段
与线段 上的动点.
上的动点.
(1)用
 表示点
表示点 到点
到点 距离;
距离;(2)设
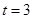 ,
,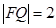 ,线段
,线段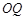 的中点在直线
的中点在直线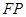 ,求
,求 的面积;
的面积;(3)设
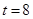 ,是否存在以
,是否存在以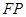 、
、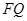 为邻边的矩形
为邻边的矩形 ,使得点
,使得点 在
在 上?若存在,求点
上?若存在,求点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.21.给定无穷数列 ,若无穷数列
,若无穷数列 满足:对任意
满足:对任意 ,都有
,都有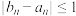 ,则称
,则称 与
与 “接近”.
“接近”.
(1)设 是首项为
是首项为 ,公比为
,公比为 的等比数列,
的等比数列, ,判断数列
,判断数列 是否
是否
与 接近,并说明理由;
接近,并说明理由;
(2)设数列 的前四项为:
的前四项为: ,
, ,
, ,
, ,
, 是一个与
是一个与 接近的数列,记集合
接近的数列,记集合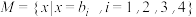 ,求
,求 中元素的个数
中元素的个数 ;
;
(3)已知 是公差为
是公差为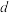 的等差数列,若存在数列
的等差数列,若存在数列 满足:
满足: 与
与 接近,且在
接近,且在 ,
,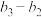 ,…,
,…, 中至少有
中至少有 个为正数,求
个为正数,求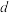 的取值范围.
的取值范围.
 ,若无穷数列
,若无穷数列 满足:对任意
满足:对任意 ,都有
,都有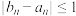 ,则称
,则称 与
与 “接近”.
“接近”.(1)设
 是首项为
是首项为 ,公比为
,公比为 的等比数列,
的等比数列, ,判断数列
,判断数列 是否
是否与
 接近,并说明理由;
接近,并说明理由;(2)设数列
 的前四项为:
的前四项为: ,
, ,
, ,
, ,
, 是一个与
是一个与 接近的数列,记集合
接近的数列,记集合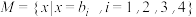 ,求
,求 中元素的个数
中元素的个数 ;
;(3)已知
 是公差为
是公差为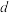 的等差数列,若存在数列
的等差数列,若存在数列 满足:
满足: 与
与 接近,且在
接近,且在 ,
, ,…,
,…, 中至少有
中至少有 个为正数,求
个为正数,求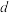 的取值范围.
的取值范围. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
