全一卷
1.设复数z满足 =i,则|z|=
=i,则|z|=
 =i,则|z|=
=i,则|z|=| A.1 | B. | C. | D.2 |
2.(2015新课标全国Ⅰ理科) =
=
 =
=A. | B. |
C.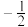 | D. |
3.设命题 ,则
,则 为
为
 ,则
,则 为
为A. | B. |
C. | D. |
4.投篮测试中,每人投3次,至少投中2次才能通过测试.已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为
| A.0.648 | B.0.432 | C.0.36 | D.0.312 |
5.已知 是双曲线
是双曲线 :
: 上的一点,
上的一点,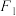 ,
,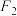 是
是 的两个焦点,若
的两个焦点,若 ,则
,则 的取值范围是
的取值范围是
 是双曲线
是双曲线 :
: 上的一点,
上的一点,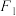 ,
,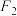 是
是 的两个焦点,若
的两个焦点,若 ,则
,则 的取值范围是
的取值范围是A. | B. | C. | D. |
6.(2015新课标全国I理科)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有


| A.14斛 | B.22斛 |
| C.36斛 | D.66斛 |
7.设 为
为 所在平面内一点,若
所在平面内一点,若 ,则下列关系中正确的是
,则下列关系中正确的是
 为
为 所在平面内一点,若
所在平面内一点,若 ,则下列关系中正确的是
,则下列关系中正确的是A. | B. |
C. | D. |
8.函数 =
= 的部分图像如图所示,则
的部分图像如图所示,则 的单调递减区间为
的单调递减区间为

 =
= 的部分图像如图所示,则
的部分图像如图所示,则 的单调递减区间为
的单调递减区间为
A. | B. |
C. | D. |
9.执行下面的程序框图,如果输入的 ,则输出的
,则输出的

 ,则输出的
,则输出的

A.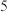 | B. | C. | D. |
10. 的展开式中,
的展开式中, 的系数为
的系数为
 的展开式中,
的展开式中, 的系数为
的系数为| A.10 | B.20 |
| C.30 | D.60 |
11.圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16 + 20 ,则r=
,则r=

 ,则r=
,则r=
| A.1 | B.2 | C.4 | D.8 |
12.设函数 ,其中
,其中 ,若存在唯一的整数
,若存在唯一的整数 ,使得
,使得 ,则
,则 的取值范围是( )
的取值范围是( )
 ,其中
,其中 ,若存在唯一的整数
,若存在唯一的整数 ,使得
,使得 ,则
,则 的取值范围是( )
的取值范围是( )A. | B. | C. | D. |
13.若函数 为偶函数,则
为偶函数,则
_____ .
 为偶函数,则
为偶函数,则
14.一个圆经过椭圆 的三个顶点,且圆心在x轴的正半轴上,则该圆的标准方程为
的三个顶点,且圆心在x轴的正半轴上,则该圆的标准方程为___________ .
 的三个顶点,且圆心在x轴的正半轴上,则该圆的标准方程为
的三个顶点,且圆心在x轴的正半轴上,则该圆的标准方程为15.若 ,
, 满足约束条件
满足约束条件 则
则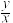 的最大值 .
的最大值 .
 ,
, 满足约束条件
满足约束条件 则
则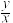 的最大值 .
的最大值 .16.如图在平面四边形ABCD中,∠A=∠B=∠C=75°,BC=2,则AB的取值范围是___________ .


17. 为数列{
为数列{ }的前
}的前 项和.已知
项和.已知 >0,
>0, =
= .
.
(Ⅰ)求{ }的通项公式;
}的通项公式;
(Ⅱ)设 ,求数列{
,求数列{ }的前
}的前 项和.
项和.
 为数列{
为数列{ }的前
}的前 项和.已知
项和.已知 >0,
>0, =
= .
.(Ⅰ)求{
 }的通项公式;
}的通项公式;(Ⅱ)设
 ,求数列{
,求数列{ }的前
}的前 项和.
项和.18.(2015新课标全国Ⅰ理科)如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.

(1)证明:平面AEC⊥平面AFC;
(2)求直线AE与直线CF所成角的余弦值.

(1)证明:平面AEC⊥平面AFC;
(2)求直线AE与直线CF所成角的余弦值.
19.某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费 和年销售量
和年销售量 (
(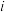 =1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值.
=1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值.

表中 ,
, =
=

(Ⅰ)根据散点图判断,y=a+bx与y=c+d 哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)已知这种产品的年利润z与x、y的关系为z=0.2y-x.根据(Ⅱ)的结果回答下列问题:
(ⅰ)年宣传费x=49时,年销售量及年利润的预报值是多少?
(ⅱ)年宣传费x为何值时,年利润的预报值最大?
附:对于一组数据 ,
, ,……,
,……, ,其回归线
,其回归线 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
 和年销售量
和年销售量 (
(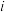 =1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值.
=1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值.
  |  |  |  |  |  |  |
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中
 ,
, =
=

(Ⅰ)根据散点图判断,y=a+bx与y=c+d
 哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)已知这种产品的年利润z与x、y的关系为z=0.2y-x.根据(Ⅱ)的结果回答下列问题:
(ⅰ)年宣传费x=49时,年销售量及年利润的预报值是多少?
(ⅱ)年宣传费x为何值时,年利润的预报值最大?
附:对于一组数据
 ,
, ,……,
,……, ,其回归线
,其回归线 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
20.在直角坐标系 中,曲线C:y=
中,曲线C:y= 与直线
与直线 交与M,N两点,
交与M,N两点,
(Ⅰ)当k=0时,分别求C在点M和N处的切线方程;
(Ⅱ)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?说明理由.
 中,曲线C:y=
中,曲线C:y= 与直线
与直线 交与M,N两点,
交与M,N两点,(Ⅰ)当k=0时,分别求C在点M和N处的切线方程;
(Ⅱ)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?说明理由.
21.已知函数 ,
, .
.
(1)当 为何值时,
为何值时, 轴为曲线
轴为曲线 的切线;
的切线;
(2)用 表示
表示 中的最小值,设函数
中的最小值,设函数 ,讨论
,讨论 零点的个数.
零点的个数.
 ,
, .
.(1)当
 为何值时,
为何值时, 轴为曲线
轴为曲线 的切线;
的切线;(2)用
 表示
表示 中的最小值,设函数
中的最小值,设函数 ,讨论
,讨论 零点的个数.
零点的个数.22.(本题满分10分)选修4-1:几何证明选讲
如图,AB是 的直径,AC是
的直径,AC是 的切线,BC交
的切线,BC交 于E.
于E.

(Ⅰ)若D为AC的中点,证明:DE是 的切线;
的切线;
(Ⅱ)若 ,求∠ACB的大小.
,求∠ACB的大小.
如图,AB是
 的直径,AC是
的直径,AC是 的切线,BC交
的切线,BC交 于E.
于E. 
(Ⅰ)若D为AC的中点,证明:DE是
 的切线;
的切线;(Ⅱ)若
 ,求∠ACB的大小.
,求∠ACB的大小. 23.在直角坐标系 中,直线
中,直线 ,圆
,圆 ,以坐标原点为极点,
,以坐标原点为极点, 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求 ,
, 的极坐标方程;
的极坐标方程;
(2)若直线 的极坐标方程为
的极坐标方程为 ,设
,设 的交点为
的交点为 ,求
,求 的面积.
的面积.
 中,直线
中,直线 ,圆
,圆 ,以坐标原点为极点,
,以坐标原点为极点, 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.(1)求
 ,
, 的极坐标方程;
的极坐标方程;(2)若直线
 的极坐标方程为
的极坐标方程为 ,设
,设 的交点为
的交点为 ,求
,求 的面积.
的面积.24.已知函数 .
.
(1)当 时,求不等式
时,求不等式 的解集;
的解集;
(2)若 的图象与
的图象与 轴围成的三角形面积大于6,求
轴围成的三角形面积大于6,求 的取值范围.
的取值范围.
 .
.(1)当
 时,求不等式
时,求不等式 的解集;
的解集;(2)若
 的图象与
的图象与 轴围成的三角形面积大于6,求
轴围成的三角形面积大于6,求 的取值范围.
的取值范围. 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
