全一卷
1.设集合A={x|-1<x<2},集合B={x|1<x<3},则A∪B=
| A.{x|-1<x<3} | B.{x|-1<x<1} | C.{x|1<x<2} | D.{x|2<x<3} |
2.设向量 =(2,4)与向量
=(2,4)与向量 =(x,6)共线,则实数x=( )
=(x,6)共线,则实数x=( )
 =(2,4)与向量
=(2,4)与向量 =(x,6)共线,则实数x=( )
=(x,6)共线,则实数x=( )| A.2 | B.3 | C.4 | D.6 |
3.某学校为了了解三年级、六年级、九年级这三个年级之间的学生视力是否存在显著差异,拟从这三个年级中按人数比例抽取部分学生进行调查,则最合理的抽样方法是
| A.抽签法 | B.系统抽样法 | C.分层抽样法 | D.随机数法 |
4.设 ,
, 是正实数,则“
是正实数,则“ ”是“
”是“ ”的
”的
 ,
, 是正实数,则“
是正实数,则“ ”是“
”是“ ”的
”的| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
5.下列函数中,最小正周期为 且图象关于原点对称的函数是( )
且图象关于原点对称的函数是( )
 且图象关于原点对称的函数是( )
且图象关于原点对称的函数是( )A. | B. |
C. | D. |
6. 执行如图所示的程序框图,输出S的值为


A.- | B. | C.- | D. |
7.过双曲线 的右焦点且与x轴垂直的直线交该双曲线的两条渐近线于A、B两点,则|AB|=( )
的右焦点且与x轴垂直的直线交该双曲线的两条渐近线于A、B两点,则|AB|=( )
 的右焦点且与x轴垂直的直线交该双曲线的两条渐近线于A、B两点,则|AB|=( )
的右焦点且与x轴垂直的直线交该双曲线的两条渐近线于A、B两点,则|AB|=( )A. | B.2 | C.6 | D.4 |
8.某食品的保鲜时间 (单位:小时)与储藏温度
(单位:小时)与储藏温度 (单位:℃)满足函数关系
(单位:℃)满足函数关系 (
( 为自然对数的底数,
为自然对数的底数, 为常数).若该食品在
为常数).若该食品在 ℃的保鲜时间是
℃的保鲜时间是 小时,在
小时,在 ℃的保鲜时间是
℃的保鲜时间是 小时,则该食品在
小时,则该食品在 ℃的保鲜时间是
℃的保鲜时间是
 (单位:小时)与储藏温度
(单位:小时)与储藏温度 (单位:℃)满足函数关系
(单位:℃)满足函数关系 (
( 为自然对数的底数,
为自然对数的底数, 为常数).若该食品在
为常数).若该食品在 ℃的保鲜时间是
℃的保鲜时间是 小时,在
小时,在 ℃的保鲜时间是
℃的保鲜时间是 小时,则该食品在
小时,则该食品在 ℃的保鲜时间是
℃的保鲜时间是| A.16小时 | B.20小时 | C.24小时 | D.21小时 |
9.
设实数x,y满足 ,则xy的最大值为( )
,则xy的最大值为( )
A. | B. |
| C.12 | D.14 |
10.设直线l与抛物线y2=4x相交于A,B两点,与圆C:(x-5)2+y2=r2(r>0)相切于点M,且M为线段AB中点,若这样的直线l恰有4条,则r的取值范围是( )
| A.(1,3) | B.(1,4) |
| C.(2,3) | D.(2,4) |
11.设i是虚数单位,则复数 =_____________.
=_____________.
 =_____________.
=_____________.12.lg0.01+log216=_____________ .
13.已知sinα+2cosα=0,则2sinαcosα-cos2α的值是______________ .
14.在三棱住ABC-A1B1C1中,∠BAC=90°,其正视图和侧视图都是边长为1的正方形,俯视图是直角边长为1的等腰直角三角形,设点M,N,P分别是AB,BC,B1C1的中点,则三棱锥P-A1MN的体积是______.
15.已知函数f(x)=2x,g(x)=x2+ax(其中a∈R).对于不相等的实数x1,x2,设m= ,n=
,n= ,现有如下命题:
,现有如下命题:
①对于任意不相等的实数x1,x2,都有m>0;
②对于任意的a及任意不相等的实数x1,x2,都有n>0;
③对于任意的a,存在不相等的实数x1,x2,使得m=n;
④对于任意的a,存在不相等的实数x1,x2,使得m=-n.
其中真命题有___________________ (写出所有真命题的序号).
 ,n=
,n= ,现有如下命题:
,现有如下命题:①对于任意不相等的实数x1,x2,都有m>0;
②对于任意的a及任意不相等的实数x1,x2,都有n>0;
③对于任意的a,存在不相等的实数x1,x2,使得m=n;
④对于任意的a,存在不相等的实数x1,x2,使得m=-n.
其中真命题有
16.设数列{an}(n=1,2,3…)的前n项和Sn满足Sn=2an-a3,且a1,a2+1,a3成等差数列.
(Ⅰ)求数列的通项公式;
(Ⅱ)设数列 的前n项和为Tn,求Tn.
的前n项和为Tn,求Tn.
(Ⅰ)求数列的通项公式;
(Ⅱ)设数列
 的前n项和为Tn,求Tn.
的前n项和为Tn,求Tn.17.一辆小客车上有5个座位,其座位号为1,2,3,4,5,乘客P1,P2,P3,P4,P5的座位号分别为1,2,3,4,5,他们按照座位号顺序先后上车,乘客P1因身体原因没有坐自己号座位,这时司机要求余下的乘客按以下规则就坐:如果自己的座位空着,就只能坐自己的座位.如果自己的座位已有乘客就坐,就在这5个座位的剩余空位中选择座位.
(1)若乘客P1坐到了3号座位,其他乘客按规则就座,则此时共有4种坐法.下表给出其中两种坐法,请填入余下两种坐法(将乘客就坐的座位号填入表中空格处)
(2)若乘客P1坐到了2号座位,其他乘客按规则就坐,求乘客P5坐到5号座位的概率.
(1)若乘客P1坐到了3号座位,其他乘客按规则就座,则此时共有4种坐法.下表给出其中两种坐法,请填入余下两种坐法(将乘客就坐的座位号填入表中空格处)
| 乘客 | P1 | P2 | P3 | P4 | P5 |
| 座位号 | 3 | 2 | 1 | 4 | 5 |
| 3 | 2 | 4 | 5 | 1 | |
18.一个正方体的平面展开图及该正方体的直观图的示意图如图所示.

(Ⅰ)请按字母F,G,H标记在正方体相应地顶点处(不需要说明理由)
(Ⅱ)判断平面BEG与平面ACH的位置关系.并说明你的结论.
(Ⅲ)证明:直线DF 平面BEG
平面BEG

(Ⅰ)请按字母F,G,H标记在正方体相应地顶点处(不需要说明理由)
(Ⅱ)判断平面BEG与平面ACH的位置关系.并说明你的结论.
(Ⅲ)证明:直线DF
 平面BEG
平面BEG19.已知A、B、C为△ABC的内角,tanA、tanB是关于方程x2+ px-p+1=0(p∈R)两个实根.
px-p+1=0(p∈R)两个实根.
(Ⅰ)求C的大小
(Ⅱ)若AB=3,AC=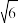 ,求p的值
,求p的值
 px-p+1=0(p∈R)两个实根.
px-p+1=0(p∈R)两个实根.(Ⅰ)求C的大小
(Ⅱ)若AB=3,AC=
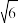 ,求p的值
,求p的值20.椭圆 (
( )的离心率是
)的离心率是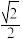 ,点
,点 在短轴
在短轴 上,且
上,且 .
.
(1)求椭圆 的方程;
的方程;
(2)设 为坐标原点,过点
为坐标原点,过点 的动直线与椭圆交于
的动直线与椭圆交于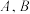 两点,是否存在常数
两点,是否存在常数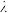 ,使得
,使得 为定值?若存在,求
为定值?若存在,求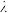 的值;若不存在,请说明理由
的值;若不存在,请说明理由
 (
( )的离心率是
)的离心率是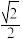 ,点
,点 在短轴
在短轴 上,且
上,且 .
.(1)求椭圆
 的方程;
的方程;(2)设
 为坐标原点,过点
为坐标原点,过点 的动直线与椭圆交于
的动直线与椭圆交于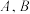 两点,是否存在常数
两点,是否存在常数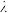 ,使得
,使得 为定值?若存在,求
为定值?若存在,求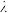 的值;若不存在,请说明理由
的值;若不存在,请说明理由21.已知函数f(x)=-2xlnx+x2-2ax+a2,其中a>0.
(Ⅰ)设g(x)为f(x)的导函数,讨论g(x)的单调性;
(Ⅱ)证明:存在a∈(0,1),使得f(x)≥0恒成立,且f(x)=0在区间(1,+∞)内有唯一解.
(Ⅰ)设g(x)为f(x)的导函数,讨论g(x)的单调性;
(Ⅱ)证明:存在a∈(0,1),使得f(x)≥0恒成立,且f(x)=0在区间(1,+∞)内有唯一解.
 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
