全一卷
1. 在点(1,
在点(1,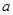 )处的切线与直线
)处的切线与直线 平行,则
平行,则 ( )
( )
 在点(1,
在点(1,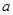 )处的切线与直线
)处的切线与直线 平行,则
平行,则 ( )
( )| A.1 | B.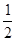 | C. | D.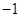 |
2.函数 的最大值为()
的最大值为()
 的最大值为()
的最大值为()| A.1 | B. | C. | D.2 |
3.若 ,且
,且 ,则
,则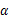 是( )
是( )
 ,且
,且 ,则
,则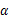 是( )
是( )| A.第一象限角 | B.第二象限角 | C.第三象限角 | D.第四象限角 |
4.等腰三角形两腰所在直线的方程分别为 与x-7y-4=0,原点在等腰三角形的底边上,则底边所在直线的斜率为().
与x-7y-4=0,原点在等腰三角形的底边上,则底边所在直线的斜率为().
 与x-7y-4=0,原点在等腰三角形的底边上,则底边所在直线的斜率为().
与x-7y-4=0,原点在等腰三角形的底边上,则底边所在直线的斜率为().| A.3 | B.2 | C. | D. |
5.设集合 ,
, ( )
( )
 ,
, ( )
( )A. | B. | C. | D. |
6.函数 的图象关于
的图象关于
 的图象关于
的图象关于A. 轴对称 轴对称 | B.直线 对称 对称 |
| C.坐标原点对称 | D.直线 对称 对称 |
7.若 ,则( )
,则( )
 ,则( )
,则( )A. < < < < | B. < < < < | C. < < < < | D. < < < < |
8.设变量 满足约束条件:
满足约束条件: ,则
,则 的最小值( )
的最小值( )
| A. | B. | C. | D. |
9.已知球的半径为2,相互垂直的两个平面分别截球面得两个圆。若两圆的公共弦长为2,则两圆的圆心距等于( )
| A.1 | B. | C. | D.2 |
10.正四棱锥的侧棱长为 ,侧棱与底面所成的角为
,侧棱与底面所成的角为 ,则该棱锥的体积为()
,则该棱锥的体积为()
 ,侧棱与底面所成的角为
,侧棱与底面所成的角为 ,则该棱锥的体积为()
,则该棱锥的体积为()| A.3 | B.6 | C.9 | D.18 |
11.设 是等腰三角形,
是等腰三角形, ,则以
,则以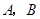 为焦点且过点
为焦点且过点 的双曲线的离心率为()
的双曲线的离心率为()
 是等腰三角形,
是等腰三角形, ,则以
,则以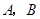 为焦点且过点
为焦点且过点 的双曲线的离心率为()
的双曲线的离心率为()A. | B. | C. | D. |
12. 的展开式中x的系数是
的展开式中x的系数是
 的展开式中x的系数是
的展开式中x的系数是A. | B. | C.3 | D.4 |
13.从10名男同学,6名女同学中选3名参加体能测试,则选到的3名同学中既有男同学又有女同学的不同选法共有______ 种(用数字作答)
14.已知 是抛物线
是抛物线 的焦点,
的焦点, 是
是 上的两个点,线段AB的中点为
上的两个点,线段AB的中点为 ,则
,则 的面积等于
的面积等于_______ .
 是抛物线
是抛物线 的焦点,
的焦点, 是
是 上的两个点,线段AB的中点为
上的两个点,线段AB的中点为 ,则
,则 的面积等于
的面积等于15.设向量 ,若向量
,若向量 与向量
与向量 共线,则
共线,则 。
。
 ,若向量
,若向量 与向量
与向量 共线,则
共线,则 。
。16.平面内的一个四边形为平行四边形的充要条件有多个,如两组对边分别平行,类似地,写出空间中的一个四棱柱为平行六面体的两个充要条件:
充要条件① ;
充要条件② 。(写出你认为正确的两个充要条件)
充要条件① ;
充要条件② 。(写出你认为正确的两个充要条件)
17.等差数列 中,
中, 且
且 成等比数列,求数列
成等比数列,求数列 前20项的和
前20项的和 .
.
 中,
中, 且
且 成等比数列,求数列
成等比数列,求数列 前20项的和
前20项的和 .
.18.如图,正四棱柱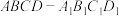 中,
中, ,点
,点 在
在 上且
上且 .
.

(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
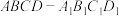 中,
中, ,点
,点 在
在 上且
上且 .
.
(Ⅰ)证明:
 平面
平面 ;
;(Ⅱ)求二面角
 的余弦值.
的余弦值.19.设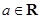 ,函数
,函数 .
.
(Ⅰ)若 是函数
是函数 的极值点,求
的极值点,求 的值;
的值;
(Ⅱ)若函数 ,在
,在 处取得最大值,求
处取得最大值,求 的取值范围.
的取值范围.
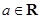 ,函数
,函数 .
.(Ⅰ)若
 是函数
是函数 的极值点,求
的极值点,求 的值;
的值;(Ⅱ)若函数
 ,在
,在 处取得最大值,求
处取得最大值,求 的取值范围.
的取值范围.20.在 中,
中, .
.
(1)求 的值;
的值;
(2)设 ,求
,求 的面积.
的面积.
 中,
中, .
.(1)求
 的值;
的值;(2)设
 ,求
,求 的面积.
的面积.21.设椭圆中心在坐标原点, 是它的两个顶点,直线
是它的两个顶点,直线 与AB相交于点D,与椭圆相交于E、F两点.
与AB相交于点D,与椭圆相交于E、F两点.
(Ⅰ)若 ,求
,求 的值;
的值;
(Ⅱ)求四边形 面积的最大值.
面积的最大值.
 是它的两个顶点,直线
是它的两个顶点,直线 与AB相交于点D,与椭圆相交于E、F两点.
与AB相交于点D,与椭圆相交于E、F两点.(Ⅰ)若
 ,求
,求 的值;
的值;(Ⅱ)求四边形
 面积的最大值.
面积的最大值.22.
甲、乙两人进行射击比赛,在一轮比赛中,甲、乙各射击一发子弹。根据以往资料知,甲击中8环,9环,10环的概率分别为0.6,0.3,0.1,乙击中8环,9环,10环的概率分别为0.4,0.4,0.2。
设甲、乙的射击相互独立。
(Ⅰ)求在一轮比赛中甲击中的环数多于乙击中环数的概率;
(Ⅱ)求在独立的三轮比赛中,至少有两轮甲击中的环数多于乙击中环数的概率。
甲、乙两人进行射击比赛,在一轮比赛中,甲、乙各射击一发子弹。根据以往资料知,甲击中8环,9环,10环的概率分别为0.6,0.3,0.1,乙击中8环,9环,10环的概率分别为0.4,0.4,0.2。
设甲、乙的射击相互独立。
(Ⅰ)求在一轮比赛中甲击中的环数多于乙击中环数的概率;
(Ⅱ)求在独立的三轮比赛中,至少有两轮甲击中的环数多于乙击中环数的概率。
 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
