搜索
全一卷
难度系数：0.65 
答案解析
有奖纠错
1．
是第三象限的角，且
，则
的值是___________.
是第三象限的角，且
，则
的值是___________.2．正四面体
的棱长为1，点
是底面
的重心，点
在线段
上，且使得
.则
的长为__________.
的棱长为1，点
是底面
的重心，点
在线段
上，且使得
.则
的长为__________.3．如图，是边长为1的正方形，点、
分别在边
、
上，
，
，
，
，其中
、
、
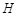、为垂足，且
.则四边形
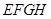的面积是___________ .
是边长为1的正方形，点、
分别在边
、
上，
，
，
，
，其中
、
、
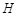、为垂足，且
.则四边形
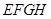的面积是
4．若
，
，
，则实数
、
、
的大小关系是____________.
，
，
，则实数
、
、
的大小关系是____________.5．原有
个同学准备在暑假中展开通信活动，每人都必须给另外
个同学写一封信，后来又有
个同学对这个活动感兴趣.若已知
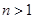，且由于增加了个同学而多写了74封信，则原有同学的人数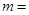
____________.
个同学准备在暑假中展开通信活动，每人都必须给另外
个同学写一封信，后来又有
个同学对这个活动感兴趣.若已知
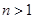，且由于增加了个同学而多写了74封信，则原有同学的人数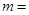
____________.6．已知、为实数，方程
的一个根为6，另一根的绝对值小于2.则抛物线
的顶点的轨迹是______________.
、为实数，方程
的一个根为6，另一根的绝对值小于2.则抛物线
的顶点的轨迹是______________.7．点
在双曲线
的右支上，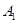
、
分别为左、右顶点，且
，则
的大小是___________度.
在双曲线
的右支上，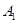
、
分别为左、右顶点，且
，则
的大小是___________度.8．如图，
是矩形的内接直角三角形，、分别在边、上，且
，
，
.则矩形面积的最小值是___________.
是矩形的内接直角三角形，、分别在边、上，且
，
，
.则矩形面积的最小值是___________.
9．数列
满足
，
，则和
的整数部分是_________.
满足
，
，则和
的整数部分是_________.10．
的值是___________.
的值是___________.11．的边长、、
同时满足下列三个条件：
（1）、、均为整数；
（2）、、组成等比数列；
（3）与中至少有一个等于100.
求出三元数组
的所有可能的解.
的边长、、
同时满足下列三个条件：（1）
、、均为整数；（2）
、、组成等比数列；（3）
与中至少有一个等于100.求出三元数组
的所有可能的解.12．设、、、
是四个不同的实数，使得
，且
.求
的最大值.
、、、
是四个不同的实数，使得
，且
.求
的最大值.13．对于平面上任意个点构成的点集，如果其中任意两点之间的距离均已确定，那么就称这个点集是“稳定的”.求证：在
格点的平面点集中，无三点共线，且其中的
个两点之间的距离已被确定，那么点集就是“稳定的”.
个点构成的点集，如果其中任意两点之间的距离均已确定，那么就称这个点集是“稳定的”.求证：在
格点的平面点集中，无三点共线，且其中的
个两点之间的距离已被确定，那么点集就是“稳定的”.