全一卷
1.设集合 ,
, ,则
,则 ( )
( )
 ,
, ,则
,则 ( )
( )A. | B. | C. | D. |
2.某中学初中部共有110名教师,高中部共有150名教师,其性别比例如图所示,则该校女教师的人数为( )


| A.167 | B.137 | C.123 | D.93 |
3.已知抛物线 的准线经过点
的准线经过点 ,则抛物线焦点坐标为
,则抛物线焦点坐标为
 的准线经过点
的准线经过点 ,则抛物线焦点坐标为
,则抛物线焦点坐标为A. | B. | C. | D. |
4.设 ,则
,则
 ,则
,则
A. | B. | C. | D. |
5.一个几何体的三视图如图所示,则该几何体的表面积为


A. | B. | C. | D. |
6.“ ”是“
”是“ ”的( )
”的( )
 ”是“
”是“ ”的( )
”的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
7.根据右边框图,当输入 为6时,输出的
为6时,输出的 ()
()

 为6时,输出的
为6时,输出的 ()
()
A. | B.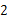 | C. | D. |
8.对任意向量 ,下列关系式中不恒成立的是
,下列关系式中不恒成立的是
 ,下列关系式中不恒成立的是
,下列关系式中不恒成立的是A. |
B. |
C. |
D. |
9.设 ,则
,则
 ,则
,则
| A.既是奇函数又是减函数 | B.既是奇函数又是增函数 |
| C.是有零点的减函数 | D.是没有零点的奇函数 |
10.设 ,若
,若 ,
, ,
, ,则下列关系式中正确的是
,则下列关系式中正确的是
 ,若
,若 ,
, ,
, ,则下列关系式中正确的是
,则下列关系式中正确的是A. | B. |
C. | D. |
11.某企业生产甲乙两种产品均需用A,B两种原料,已知生产1吨每种产品需原料及每天原料的可用限额如表所示,如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为()


| A.12万元 | B.16万元 | C.17万元 | D.18万元 |
12.设复数 ,若
,若 ,则
,则 的概率为( )
的概率为( )
 ,若
,若 ,则
,则 的概率为( )
的概率为( )A. | B. | C. | D. |
13.中位数为1010的一组数构成等差数列,其末项为 2015,则该数列的首项为__________ .
14.如图,某港口一天6时到18时的水深变化曲线近似满足函数y=3sin( x+Φ)+k,据此函数可知,这段时间水深(单位:m)的最大值为____________.
x+Φ)+k,据此函数可知,这段时间水深(单位:m)的最大值为____________.

 x+Φ)+k,据此函数可知,这段时间水深(单位:m)的最大值为____________.
x+Φ)+k,据此函数可知,这段时间水深(单位:m)的最大值为____________.
15.函数 在其极值点处的切线方程为
在其极值点处的切线方程为____________ .
 在其极值点处的切线方程为
在其极值点处的切线方程为16.观察下列等式:

据此规律,第 个等式可写为 ________.
个等式可写为 ________.

据此规律,第
 个等式可写为 ________.
个等式可写为 ________.17. 的内角
的内角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, .向量
.向量 与
与 平行.
平行.
(Ⅰ)求 ;
;
(Ⅱ)若 ,
, 求
求 的面积.
的面积.
 的内角
的内角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, .向量
.向量 与
与 平行.
平行.(Ⅰ)求
 ;
;(Ⅱ)若
 ,
, 求
求 的面积.
的面积.18.如图1,在直角梯形 中,
中,
 ,
, 是
是 的中点,
的中点, 是
是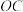 与
与 的交点,将
的交点,将 沿
沿 折起到图2中
折起到图2中 的位置,得到四棱锥
的位置,得到四棱锥 .
.

(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)当平面 平面
平面 时,四棱锥
时,四棱锥 的体积为
的体积为 ,求
,求 的值.
的值.
 中,
中,
 ,
, 是
是 的中点,
的中点, 是
是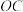 与
与 的交点,将
的交点,将 沿
沿 折起到图2中
折起到图2中 的位置,得到四棱锥
的位置,得到四棱锥 .
.
(Ⅰ)证明:
 平面
平面 ;
;(Ⅱ)当平面
 平面
平面 时,四棱锥
时,四棱锥 的体积为
的体积为 ,求
,求 的值.
的值.19.随机抽取往年的一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
(1)在今年4月份任取一天,估计西安市在该天不下雨的概率;
(2)西安市某学校拟从今年4月份的一个晴天开始举行连续两天的运动会,估计运动会期间不下雨的概率.
| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天气 | 晴 | 雨 | 阴 | 阴 | 阴 | 雨 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 晴 |
| 日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 天气 | 晴 | 阴 | 雨 | 阴 | 阴 | 晴 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 雨 |
(1)在今年4月份任取一天,估计西安市在该天不下雨的概率;
(2)西安市某学校拟从今年4月份的一个晴天开始举行连续两天的运动会,估计运动会期间不下雨的概率.
20.如图,椭圆 经过点
经过点 ,且离心率为
,且离心率为 .
.
(I)求椭圆 的方程;
的方程;
(II)经过点 ,且斜率为
,且斜率为 的直线与椭圆
的直线与椭圆 交于不同两点
交于不同两点 (均异于点
(均异于点 ),
),
问:直线 与
与 的斜率之和是否为定值?若是,求出此定值;若否,说明理由.
的斜率之和是否为定值?若是,求出此定值;若否,说明理由.

 经过点
经过点 ,且离心率为
,且离心率为 .
.(I)求椭圆
 的方程;
的方程;(II)经过点
 ,且斜率为
,且斜率为 的直线与椭圆
的直线与椭圆 交于不同两点
交于不同两点 (均异于点
(均异于点 ),
),问:直线
 与
与 的斜率之和是否为定值?若是,求出此定值;若否,说明理由.
的斜率之和是否为定值?若是,求出此定值;若否,说明理由.
21.设
(Ⅰ)求 ;
;
(Ⅱ)证明: 在
在 内有且仅有一个零点(记为
内有且仅有一个零点(记为 ),且
),且 .
.

(Ⅰ)求
 ;
;(Ⅱ)证明:
 在
在 内有且仅有一个零点(记为
内有且仅有一个零点(记为 ),且
),且 .
.22.选修4-1:几何证明选讲
如图, 切
切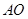 于点
于点 ,直线
,直线 交
交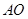 于
于 两点,
两点, 垂足为
垂足为 .
.

(Ⅰ)证明:
(Ⅱ)若 ,求
,求 的直径.
的直径.
如图,
 切
切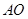 于点
于点 ,直线
,直线 交
交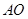 于
于 两点,
两点, 垂足为
垂足为 .
.
(Ⅰ)证明:

(Ⅱ)若
 ,求
,求 的直径.
的直径.23.选修4-4:坐标系与参数方程
在直角坐标系 中,直线
中,直线 的参数方程为
的参数方程为 (
( 为参数).以原点为极点,
为参数).以原点为极点, 轴正半轴为极
轴正半轴为极
轴建立极坐标系, 的极坐标方程为
的极坐标方程为 .
.
(Ⅰ)写出 的直角坐标方程;
的直角坐标方程;
(Ⅱ) 为直线
为直线 上一动点,当
上一动点,当 到圆心
到圆心 的距离最小时,求
的距离最小时,求 的直角坐标.
的直角坐标.
在直角坐标系
 中,直线
中,直线 的参数方程为
的参数方程为 (
( 为参数).以原点为极点,
为参数).以原点为极点, 轴正半轴为极
轴正半轴为极轴建立极坐标系,
 的极坐标方程为
的极坐标方程为 .
.(Ⅰ)写出
 的直角坐标方程;
的直角坐标方程;(Ⅱ)
 为直线
为直线 上一动点,当
上一动点,当 到圆心
到圆心 的距离最小时,求
的距离最小时,求 的直角坐标.
的直角坐标.24.已知关于 的不等式
的不等式 的解集为
的解集为
(1)求实数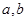 的值;
的值;
(2)求 的最大值.
的最大值.
 的不等式
的不等式 的解集为
的解集为
(1)求实数
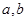 的值;
的值;(2)求
 的最大值.
的最大值. 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
