全一卷
1.下列互为倒数的是( )
A. 和 和 | B. 和 和 | C. 和 和 | D. 和 和 |
2.下列图形中,主视图和左视图一样的是( )
A. | B. | C. | D. |
3.某学校进行演讲比赛,最终有7位同学进入决赛,这七位同学的评分分别是:9.5,9.3,9.1,9.4,9.7,9.3,9.6.请问这组评分的众数是( )
| A.9.5 | B.9.4 | C.9.1 | D.9.3 |
4.某公司一年的销售利润是1.5万亿元.1.5万亿用科学记数法表示( )
A. | B. | C. | D. |
5.下列运算正确的是( )
A. | B. | C. | D. |
6.一元一次不等式组 的解集为( )
的解集为( )
 的解集为( )
的解集为( )A. | B. |
C. | D. |
7.将一副三角板如图所示放置,斜边平行,则 的度数为( )
的度数为( )

 的度数为( )
的度数为( )
A. | B. | C. | D. |
8.下列说法错误 的是( )
| A.对角线垂直且互相平分的四边形是菱形 | B.同圆或等圆中,同弧对应的圆周角相等 |
| C.对角线相等的四边形是矩形 | D.对角线垂直且相等的平行四边形是正方形 |
9.张三经营了一家草场,草场里面种植上等草和下等草.他卖五捆上等草的根数减去11根,就等于七捆下等草的根数;卖七捆上等草的根数减去25根,就等于五捆下等草的根数.设上等草一捆为 根,下等草一捆为
根,下等草一捆为 根,则下列方程正确的是( )
根,则下列方程正确的是( )
 根,下等草一捆为
根,下等草一捆为 根,则下列方程正确的是( )
根,则下列方程正确的是( )A. | B. | C. | D. |
10.如图所示,已知三角形 为直角三角形,
为直角三角形, ,BC为
,BC为 切线,
切线, 为切点,
为切点, 为
为 直径,
直径, 则
则 和
和 面积之比为( )
面积之比为( )

 为直角三角形,
为直角三角形, ,BC为
,BC为 切线,
切线, 为切点,
为切点, 为
为 直径,
直径, 则
则 和
和 面积之比为( )
面积之比为( )
A. | B. | C. | D. |
11.分解因式: =
=____ .
 =
=12.某工厂一共有1200人,为选拔人才,提出了一些选拔的条件,并进行了抽样调查.从中抽出400人,发现有300人是符合条件的,那么则该工厂1200人中符合选拔条件的人数为________________ .
13.已知一元二次方程 有两个相等的实数根,则
有两个相等的实数根,则 的值为
的值为________________ .
 有两个相等的实数根,则
有两个相等的实数根,则 的值为
的值为14.如图,已知直角三角形 中,
中, ,将
,将 绕点
绕点 点旋转至
点旋转至 的位置,且
的位置,且 在
在 的中点,
的中点, 在反比例函数
在反比例函数 上,则
上,则 的值为
的值为________________ .

 中,
中, ,将
,将 绕点
绕点 点旋转至
点旋转至 的位置,且
的位置,且 在
在 的中点,
的中点, 在反比例函数
在反比例函数 上,则
上,则 的值为
的值为
15.已知 是直角三角形,
是直角三角形, 连接
连接 以
以 为底作直角三角形
为底作直角三角形 且
且
 是
是 边上的一点,连接
边上的一点,连接 和
和
 且
且 则
则 长为
长为______ .

 是直角三角形,
是直角三角形, 连接
连接 以
以 为底作直角三角形
为底作直角三角形 且
且
 是
是 边上的一点,连接
边上的一点,连接 和
和
 且
且 则
则 长为
长为
16.

17.先化简,再求值: 其中
其中
 其中
其中
18.某工厂进行厂长选拔,从中抽出一部分人进行筛选,其中有“优秀”,“良好”,“合格”,“不合格”.

(1)本次抽查总人数为 ,“合格”人数的百分比为 .
(2)补全条形统计图.
(3)扇形统计图中“不合格人数”的度数为 .
(4)在“优秀”中有甲乙丙三人,现从中抽出两人,则刚好抽中甲乙两人的概率为 .

(1)本次抽查总人数为 ,“合格”人数的百分比为 .
(2)补全条形统计图.
(3)扇形统计图中“不合格人数”的度数为 .
(4)在“优秀”中有甲乙丙三人,现从中抽出两人,则刚好抽中甲乙两人的概率为 .
19.某学校打算购买甲乙两种不同类型的笔记本.已知甲种类型的笔记本的单价比乙种类型的要便宜1元,且用110元购买的甲种类型的数量与用120元购买的乙种类型的数量一样.
(1)求甲乙两种类型笔记本的单价.
(2)该学校打算购买甲乙两种类型笔记本共100件,且购买的乙的数量不超过甲的3倍,则购买的最低费用是多少?
(1)求甲乙两种类型笔记本的单价.
(2)该学校打算购买甲乙两种类型笔记本共100件,且购买的乙的数量不超过甲的3倍,则购买的最低费用是多少?
20.二次函数 先向上平移6个单位,再向右平移3个单位,用光滑的曲线画在平面直角坐标系上.
先向上平移6个单位,再向右平移3个单位,用光滑的曲线画在平面直角坐标系上.

(1) 的值为 ;
的值为 ;
(2)在坐标系中画出平移后的图象并求出 与
与 的交点坐标;
的交点坐标;
(3)点 在新的函数图象上,且
在新的函数图象上,且 两点均在对称轴的同一侧,若
两点均在对称轴的同一侧,若 则
则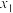
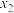 (填“
(填“ ”或“
”或“ ”或“
”或“ ”)
”)
 先向上平移6个单位,再向右平移3个单位,用光滑的曲线画在平面直角坐标系上.
先向上平移6个单位,再向右平移3个单位,用光滑的曲线画在平面直角坐标系上.
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
(1)
 的值为 ;
的值为 ;(2)在坐标系中画出平移后的图象并求出
 与
与 的交点坐标;
的交点坐标;(3)点
 在新的函数图象上,且
在新的函数图象上,且 两点均在对称轴的同一侧,若
两点均在对称轴的同一侧,若 则
则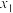
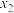 (填“
(填“ ”或“
”或“ ”或“
”或“ ”)
”)21.一个玻璃球体近似半圆 为直径,半圆
为直径,半圆 上点
上点 处有个吊灯
处有个吊灯

 的中点为
的中点为

(1)如图①, 为一条拉线,
为一条拉线, 在
在 上,
上, 求
求 的长度.
的长度.
(2)如图②,一个玻璃镜与圆 相切,
相切, 为切点,
为切点, 为
为 上一点,
上一点, 为入射光线,
为入射光线, 为反射光线,
为反射光线, 求
求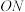 的长度.
的长度.
(3)如图③, 是线段
是线段 上的动点,
上的动点, 为入射光线,
为入射光线, 为反射光线交圆
为反射光线交圆 于点
于点 在
在 从
从 运动到
运动到 的过程中,求
的过程中,求 点的运动路径长.
点的运动路径长.
 为直径,半圆
为直径,半圆 上点
上点 处有个吊灯
处有个吊灯

 的中点为
的中点为

(1)如图①,
 为一条拉线,
为一条拉线, 在
在 上,
上, 求
求 的长度.
的长度.(2)如图②,一个玻璃镜与圆
 相切,
相切, 为切点,
为切点, 为
为 上一点,
上一点, 为入射光线,
为入射光线, 为反射光线,
为反射光线, 求
求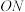 的长度.
的长度.(3)如图③,
 是线段
是线段 上的动点,
上的动点, 为入射光线,
为入射光线, 为反射光线交圆
为反射光线交圆 于点
于点 在
在 从
从 运动到
运动到 的过程中,求
的过程中,求 点的运动路径长.
点的运动路径长.22.(1)【探究发现】如图①所示,在正方形 中,
中, 为
为 边上一点,将
边上一点,将 沿
沿 翻折到
翻折到 处,延长
处,延长 交
交 边于
边于 点.求证:
点.求证:

(2)【类比迁移】如图②,在矩形 中,
中, 为
为 边上一点,且
边上一点,且 将
将 沿
沿 翻折到
翻折到 处,延长
处,延长 交
交 边于点
边于点 延长
延长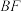 交
交 边于点
边于点 且
且 求
求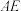 的长.
的长.

(3)【拓展应用】如图③,在菱形 中,
中,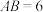 ,
, 为
为 边上的三等分点,
边上的三等分点, 将
将 沿
沿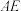 翻折得到
翻折得到 ,直线
,直线 交
交 于点
于点 求
求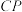 的长.
的长.

 中,
中, 为
为 边上一点,将
边上一点,将 沿
沿 翻折到
翻折到 处,延长
处,延长 交
交 边于
边于 点.求证:
点.求证:

(2)【类比迁移】如图②,在矩形
 中,
中, 为
为 边上一点,且
边上一点,且 将
将 沿
沿 翻折到
翻折到 处,延长
处,延长 交
交 边于点
边于点 延长
延长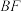 交
交 边于点
边于点 且
且 求
求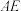 的长.
的长.
(3)【拓展应用】如图③,在菱形
 中,
中,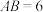 ,
, 为
为 边上的三等分点,
边上的三等分点, 将
将 沿
沿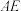 翻折得到
翻折得到 ,直线
,直线 交
交 于点
于点 求
求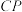 的长.
的长.
 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
