搜索
全一卷
难度系数：0.85 
答案解析
有奖纠错
1．下列各数中，最小的数是
| A．0 | B． | C． | D． |
2．据统计，2013年河南省旅游业总收入达到约3875.5亿元，若将3875.5亿用科学记数法表示为3.8755×10n，则n等于（ ）
| A．10 | B．11 | C．12 | D．13 |
3．如图，直线AB，CD相交于点O，射线OM平分∠AOC，ON⊥OM，若∠AOM=35°，则∠CON的度数为（ ）
| A．35° | B．45° | C．55° | D．65° |
4．下列各式计算正确的是（ ）
A． | B． | C． | D． |
5．下列说法中，正确的是（ ）
| A．“打开电视，正在播放河南新闻节目”是必然事件 |
| B．某种彩票中奖概率为10%是指买十张一定有一张中奖 |
| C．神舟飞船发射前要对各部件进行抽样检查 |
| D．了解某种节能灯的使用寿命适合抽样调查 |
6．将两个长方体如图放置，则所构成的几何体的左视图可能是 （ ）
A． | B． | C． | D． |
7．如图，▱ABCD的对角线AC与BD相交于点O，AB⊥AC，若AB＝4，AC＝6，则BD的长是（ ）
| A．8 | B．9 | C．10 | D．11 |
8．如图，在Rt
ABC中，
C=90°，AC=1cm，BC=2cm，点P从A出发，以1cm/s的速沿折线AC→CB→BA运动，最终回到A点．设点P的运动时间为x(s)，线段AP的长度为y(cm)，则能反映y与x之间函数关系的图像大致是（ ）
ABC中，
C=90°，AC=1cm，BC=2cm，点P从A出发，以1cm/s的速沿折线AC→CB→BA运动，最终回到A点．设点P的运动时间为x(s)，线段AP的长度为y(cm)，则能反映y与x之间函数关系的图像大致是（ ）
A． | B． |
C． | D． |
9．计算：
______ ．
10．不等式组
的所有整数解的和为_________ ．
的所有整数解的和为11．如图，在
中，按以下步骤作图：①分别以B，C为圆心，以大于
BC的长为半径作弧，两弧相交于M，N两点；②作直线MN交AB于点D，连接CD，若CD＝AC，∠B＝25
，则∠ACB的度数为_____ ．
中，按以下步骤作图：①分别以B，C为圆心，以大于
BC的长为半径作弧，两弧相交于M，N两点；②作直线MN交AB于点D，连接CD，若CD＝AC，∠B＝25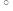
，则∠ACB的度数为
12．已知抛物线y＝ax2＋bx＋c(a≠0)与x轴交于A，B两点．若点A的坐标为(－2，0)，抛物线的对称轴为直线x＝2，则线段AB的长为___________ ．
13．一个不透明的袋子中装有仅颜色不同的2个红球和2个白球，两个人依次从袋子中随机摸出一个小球不放回，则第一个人摸到红球且第二个人摸到白球的概率是________ ．
14．如图，在菱形ABCD中，AB=1，∠DAB=60°，把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′，其中点C的运动路径为
，则图中阴影部分的面积为__ ．
，则图中阴影部分的面积为
15．如图，矩形ABCD中，AD=5，AB=7，点E为DC上一个动点，把△ADE沿AE折叠，当点D的对应点D'落在∠ABC的角平分线上时，DE的长为____ ．
16．先化简，再求值：
，其中x=
-1．
，其中x=
-1．17．如图，CD是⊙O的直径，且CD=2cm，点P为CD的延长线上一点，过点P作⊙O的切线PA，PB，切点分别为点A，B．
(1)连接AC，若∠APO=30°，试证明△ACP是等腰三角形；
(2)填空：
①当DP= cm时，四边形AOBD是菱形；
②当DP= cm时，四边形AOBP是正方形．
(1)连接AC，若∠APO=30°，试证明△ACP是等腰三角形；
(2)填空：
①当DP= cm时，四边形AOBD是菱形；
②当DP= cm时，四边形AOBP是正方形．
18．某兴趣小组为了了解本校男生参加课外体育锻炼情况，随机抽取本校300名男生进行了问卷调查，统计整理并绘制了如下两幅尚不完整的统计图．
请根据以上信息解答下列问题：
（1）课外体育锻炼情况扇形统计图中，“经常参加”所对应的圆心角的度数为______；
（2）请补全条形统计图；
（3）该校共有1200名男生，请估计全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数；
（4）小明认为“全校所有男生中，课外最喜欢参加的运动项目 是乒乓球的人数约为
”，请你判断这种说法是否正确，并说明理由．
请根据以上信息解答下列问题：
（1）课外体育锻炼情况扇形统计图中，“经常参加”所对应的圆心角的度数为______；
（2）请补全条形统计图；
（3）该校共有1200名男生，请估计全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数；
（4）小明认为“全校所有男生中，
”，请你判断这种说法是否正确，并说明理由．19．在中俄“海上联合﹣2014”反潜演习中，我军舰A测得潜艇C的俯角为30°，位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°，试根据以上数据求出潜艇C离开海平面的下潜深度．（结果保留整数，参考数据：sin68°≈0.9，cos68°≈0.4，tan68°≈2.5，
1.7）
1.7）
20．如图，在直角梯形OABC中，BC∥AO，∠AOC＝90°，点A，B的坐标分别为（5，0），（2，6），点D为AB上一点，且BD＝2AD，双曲线y＝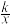
（k＞0）经过点D，交BC于点E．
（1）求双曲线的解析式；
（2）求四边形ODBE的面积．
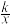（k＞0）经过点D，交BC于点E．（1）求双曲线的解析式；
（2）求四边形ODBE的面积．
21．某商店销售10台
型和20台
型电脑的利润为4000元，销售20台型和10台型电脑的利润为3500元．
（1）求每台型电脑和型电脑的销售利润；
（2）该商店计划一次购进两种型号的电脑共100台，其中型电脑的进货量不超过型电脑的2倍，设购进型电脑
台，这100台电脑的销售总利润为
元；
①求关于的函数关系式；
②该商店购进型、型电脑各多少台，才能使销售总利润最大？
（3）实际进货时，厂家对型电脑出厂价下调
元，且限定商店最多购进型电脑70台，若商店保持同种电脑的售价不变，请你根据以上信息及（2）中条件，设计出使这100台电脑销售总利润最大的进货方案．
型和20台
型电脑的利润为4000元，销售20台型和10台型电脑的利润为3500元．（1）求每台
型电脑和型电脑的销售利润；（2）该商店计划一次购进两种型号的电脑共100台，其中
型电脑的进货量不超过型电脑的2倍，设购进型电脑
台，这100台电脑的销售总利润为
元；①求
关于的函数关系式；②该商店购进
型、型电脑各多少台，才能使销售总利润最大？（3）实际进货时，厂家对
型电脑出厂价下调
元，且限定商店最多购进型电脑70台，若商店保持同种电脑的售价不变，请你根据以上信息及（2）中条件，设计出使这100台电脑销售总利润最大的进货方案．22．探究题:
(1)如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE，则
的度数为______；线段AD，BE之间的数量关系为______；
(2)如图2，△ACB和△DCE均为等腰三角形，
，点A，D，E在同一直线上，CM为△DCE中DE边上的高，连接BE，请猜测的度数及线段CM，AE，BE之间的数量关系，并说明理由．
(3)如图3，在正方形ABCD中，
，若点P满足
，且
，请直接写出点A到BP的距离．
(1)如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE，则
的度数为______；线段AD，BE之间的数量关系为______；(2)如图2，△ACB和△DCE均为等腰三角形，
，点A，D，E在同一直线上，CM为△DCE中DE边上的高，连接BE，请猜测的度数及线段CM，AE，BE之间的数量关系，并说明理由．(3)如图3，在正方形ABCD中，
，若点P满足
，且
，请直接写出点A到BP的距离．23．如图，抛物线y=﹣x2+bx+c与x轴交于点A（﹣1，0），B（5，0）两点，直线y=﹣
x+3与y轴交于点C，与x轴交于点D．点P是x轴上方的抛物线上一动点，过点P作PF⊥x轴于点F，交直线CD于点E．设点P的横坐标为m．
(1)求抛物线的解析式；
(2)若PE=5EF，求m的值；
(3)若点E′是点E关于直线PC的对称点，是否存在点P，使点E′落在y轴上？若存在，请直接写出相应的点P的坐标；若不存在，请说明理由．
x+3与y轴交于点C，与x轴交于点D．点P是x轴上方的抛物线上一动点，过点P作PF⊥x轴于点F，交直线CD于点E．设点P的横坐标为m．(1)求抛物线的解析式；
(2)若PE=5EF，求m的值；
(3)若点E′是点E关于直线PC的对称点，是否存在点P，使点E′落在y轴上？若存在，请直接写出相应的点P的坐标；若不存在，请说明理由．
