搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．﹣6的相反数是（ ）
| A．﹣6 | B．﹣ | C．6 | D． |
2．某4S店今年1～5月新能源汽车的销量（辆数）分别如下：25，33，36，31，40，这组数据的平均数是（ ）
| A．34 | B．33 | C．32.5 | D．31 |
3．下列运算正确的是（ ）
| A．a2+a3＝a5 | B．（a3）2＝a6 |
| C．（a﹣b）2＝a2﹣b2 | D．x6÷x3＝x2 |
4．2022年2月第24届冬季奥林匹克运动会在我国北京成功举办，以下是参选的冬奥会会徽设计的部分图形，其中既是轴对称图形又是中心对称图形的是（ ）
A． | B． |
C． | D． |
5．下列说法错误的是（ ）
| A．打开电视机，中央台正在播放发射神舟十四号载人飞船的新闻，这是随机事件 |
| B．要了解小王一家三口的身体健康状况，适合采用抽样调查 |
| C．一组数据的方差越小，它的波动越小 |
| D．样本中个体的数目称为样本容量 |
6．如图是正方体的表面展开图，则与“话”字相对的字是（ ）
| A．跟 | B．党 | C．走 | D．听 |
7．如图，在▱ABCD中，已知AB＝12，AD＝8，∠ABC的平分线BM交CD边于点M，则DM的长为（ ）
| A．2 | B．4 | C．6 | D．8 |
8．如图，数轴上的两点A、B对应的实数分别是a、b，则下列式子中成立的是（ ）
| A．1﹣2a＞1﹣2b | B．﹣a＜﹣b | C．a+b＜0 | D．|a|﹣|b|＞0 |
9．如图，在平面直角坐标系中，点B、C、E在y轴上，点C的坐标为（0，1），AC＝2，Rt△ODE是Rt△ABC经过某些变换得到的，则正确的变换是（ ）
| A．△ABC绕点C逆时针旋转90°，再向下平移1个单位 |
| B．△ABC绕点C顺时针旋转90°，再向下平移1个单位 |
| C．△ABC绕点C逆时针旋转90°，再向下平移3个单位 |
| D．△ABC绕点C顺时针旋转90°，再向下平移3个单位 |
10．如图，在平面直角坐标系中，点M为x轴正半轴上一点，过点M的直线l∥y轴，且直线l分别与反比例函数
和
的图象交于P、Q两点．若S△POQ＝15，则k的值为（ ）
和的图象交于P、Q两点．若S△POQ＝15，则k的值为（ ） | A．38 | B．22 | C．﹣7 | D．﹣22 |
11．如图，正六边形ABCDEF内接于⊙O，半径为6，则这个正六边形的边心距OM和
的长分别为（ ）
的长分别为（ ）A．4， | B．3 ，π | C．2， | D．3，2π |
12．如图，抛物线y＝ax2+bx+c与x轴交于两点（x1，0）、（2，0），其中0＜x1＜1．下列四个结论：①abc＜0；②a+b+c＞0；③2a﹣c＞0；④不等式ax2+bx+c＞﹣
x+c的解集为0＜x＜x1．其中正确结论的个数是（ ）
x+c的解集为0＜x＜x1．其中正确结论的个数是（ ）
| A．4 | B．3 | C．2 | D．1 |
13．函数
中，自变量
的取值范围是_______ .
中，自变量的取值范围是14．如图，在⊙O中，∠ABC=50°，则∠AOC等于_____
15．对于非零实数a，b，规定a⊕b＝
，若（2x﹣1）⊕2＝1，则x的值为 _____ ．
，若（2x﹣1）⊕2＝1，则x的值为 16．勾股定理被记载于我国古代的数学著作《周髀算经》中，汉代数学家赵爽为了证明勾股定理，创制了一幅如图①所示的“弦图”，后人称之为“赵爽弦图”．图②由弦图变化得到，它是由八个全等的直角三角形拼接而成．记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3．若正方形EFGH的边长为4，则S1+S2+S3＝_____ ．
17．分解因式：a4﹣3a2﹣4＝_____ ．
18．如图，在平面直角坐标系中，一次函数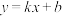
的图象经过点
且与函数
的图象交于点
.若一次函数
随
的增大而增大，则
的取值范围是____ ．
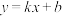的图象经过点
且与函数
的图象交于点
.若一次函数
随
的增大而增大，则
的取值范围是
19．已知x1、x2是关于x的方程x2﹣2x+k﹣1＝0的两实数根，且
＝x12+2x2﹣1，则k的值为 _____ ．
＝x12+2x2﹣1，则k的值为 20．如图，矩形ABCD中，AB＝6，AD＝4，点E、F分别是AB、DC上的动点，EF∥BC，则AF+CE的最小值是 _____ ．
21．（1）计算：
；
（2）先化简，再求值：（
）÷
，其中a＝﹣
，b＝+4．
；（2）先化简，再求值：（
）÷，其中a＝﹣，b＝+4．22．如图，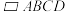
中，E、F是对角线BD上两个点，且满足BE=DF．
（1）求证：△ABE≌△CDF；
（2）求证：四边形AECF是平行四边形．
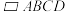中，E、F是对角线BD上两个点，且满足BE=DF．（1）求证：△ABE≌△CDF；
（2）求证：四边形AECF是平行四边形．
23．为让同学们了解新冠病毒的危害及预防措施，某中学举行了“新冠病毒预防”知识竞赛．数学课外活动小组将八（1）班参加本校知识竞赛的40名同学的成绩（满分为100分，得分为正整数且无满分，最低为75分）分成五组进行统计，并绘制了下列不完整的统计图表：
(1)表中m＝ ，n＝ ；
(2)请补全频数分布直方图；
(3)本次知识竞赛中，成绩在94.5分以上的选手，男生和女生各占一半，从中随机确定2名学生参加颁奖，请用列表法或树状图法求恰好是一名男生和一名女生的概率．
分数段 | 频数 | 频率 |
74.5﹣79.5 | 2 | 0.05 |
79.5﹣84.5 | 8 | n |
84.5﹣89.5 | 12 | 0.3 |
89.5﹣94.5 | m | 0.35 |
94.5﹣99.5 | 4 | 0.1 |
(1)表中m＝ ，n＝ ；
(2)请补全频数分布直方图；
(3)本次知识竞赛中，成绩在94.5分以上的选手，男生和女生各占一半，从中随机确定2名学生参加颁奖，请用列表法或树状图法求恰好是一名男生和一名女生的概率．
24．如图所示，九（1）班数学兴趣小组为了测量河对岸的古树A、B之间的距离，他们在河边与AB平行的直线l上取相距60m的C、D两点，测得∠ACB＝15°，∠BCD＝120°，∠ADC＝30°．
(1)求河的宽度；
(2)求古树A、B之间的距离．（结果保留根号）
(1)求河的宽度；
(2)求古树A、B之间的距离．（结果保留根号）
25．如图，△ABC内接于⊙O，AB是⊙O的直径，⊙O的切线PC交BA的延长线于点P，OF∥BC交AC于点E，交PC于点F，连接AF．
(1)判断直线AF与⊙O的位置关系并说明理由；
(2)若⊙O的半径为6，AF＝2，求AC的长；
(3)在（2）的条件下，求阴影部分的面积．
(1)判断直线AF与⊙O的位置关系并说明理由；
(2)若⊙O的半径为6，AF＝2
，求AC的长；(3)在（2）的条件下，求阴影部分的面积．
26．为贯彻执行“德、智、体、美、劳”五育并举的教育方针，内江市某中学组织全体学生前往某劳动实践基地开展劳动实践活动．在此次活动中，若每位老师带队30名学生，则还剩7名学生没老师带；若每位老师带队31名学生，就有一位老师少带1名学生．现有甲、乙两型客车，它们的载客量和租金如表所示：
学校计划此次劳动实践活动的租金总费用不超过3000元．
(1)参加此次劳动实践活动的老师和学生各有多少人？
(2)每位老师负责一辆车的组织工作，请问有哪几种租车方案？
(3)学校租车总费用最少是多少元？
| 甲型客车 | 乙型客车 | |
| 载客量（人/辆） | 35 | 30 |
| 租金（元/辆） | 400 | 320 |
(1)参加此次劳动实践活动的老师和学生各有多少人？
(2)每位老师负责一辆车的组织工作，请问有哪几种租车方案？
(3)学校租车总费用最少是多少元？
27．如图，在矩形ABCD中，AB＝6，BC＝4，点M、N分别在AB、AD上，且MN⊥MC，点E为CD的中点，连接BE交MC于点F．
(1)当F为BE的中点时，求证：AM＝CE；
(2)若
＝2，求
的值；
(3)若MN∥BE，求的值．
(1)当F为BE的中点时，求证：AM＝CE；
(2)若
＝2，求
的值；(3)若MN∥BE，求
的值．28．如图，抛物线y＝ax2+bx+c与x轴交于A（﹣4，0），B（2，0），与y轴交于点C（0，2）．
(1)求这条抛物线所对应的函数的表达式；
(2)若点D为该抛物线上的一个动点，且在直线AC上方，求点D到直线AC的距离的最大值及此时点D的坐标；
(3)点P为抛物线上一点，连接CP，直线CP把四边形CBPA的面积分为1：5两部分，求点P的坐标．
(1)求这条抛物线所对应的函数的表达式；
(2)若点D为该抛物线上的一个动点，且在直线AC上方，求点D到直线AC的距离的最大值及此时点D的坐标；
(3)点P为抛物线上一点，连接CP，直线CP把四边形CBPA的面积分为1：5两部分，求点P的坐标．
