全一卷
1. ( )
( )
 ( )
( )A. | B. | C. | D.2 |
2.2022年5月,四川省发展和改革委员会下达了保障性安居工程2022年第一批中央预算内投资计划,泸州市获得75500000元中央预算内资金支持,将75500000用科学记数法表示为( )
A. | B. |
C. | D. |
3.如图是一个由6个大小相同的正方体组成的几何体,它的俯视图是( )


A. | B. |
C. | D. |
4.如图,直线 ,直线
,直线 分别交
分别交 于点
于点 ,点
,点 在直线
在直线 上,
上, ,若
,若 ,则
,则 的度数是( )
的度数是( )

 ,直线
,直线 分别交
分别交 于点
于点 ,点
,点 在直线
在直线 上,
上, ,若
,若 ,则
,则 的度数是( )
的度数是( )
A. | B. | C. | D. |
5.下列运算正确的是( )
A. | B. |
C. | D. |
6.费尔兹奖是国际上享有崇高声誉的一个数学奖项,每四年评选一次,主要授予年轻的数学家.下面数据是部分获奖者获奖时的年龄(单位:岁):29,32,33,35,35,40,则这组数据的众数和中位数分别是( )
| A.35,35 | B.34,33 | C.34,35 | D.35,34 |
7.与 最接近的整数是( )
最接近的整数是( )
 最接近的整数是( )
最接近的整数是( )| A.4 | B.5 | C.6 | D.7 |
8.抛物线 经平移后,不可能得到的抛物线是( )
经平移后,不可能得到的抛物线是( )
 经平移后,不可能得到的抛物线是( )
经平移后,不可能得到的抛物线是( )A. | B. |
C. | D. |
9.已知关于 的方程
的方程 的两实数根为
的两实数根为 ,
, ,若
,若 ,则
,则 的值为( )
的值为( )
 的方程
的方程 的两实数根为
的两实数根为 ,
, ,若
,若 ,则
,则 的值为( )
的值为( )A. | B. | C. 或3 或3 | D. 或3 或3 |
10.如图, 是
是 的直径,
的直径, 垂直于弦
垂直于弦 于点
于点 ,
, 的延长线交
的延长线交 于点
于点 .若
.若 ,
, ,则
,则 的长是( )
的长是( )

 是
是 的直径,
的直径, 垂直于弦
垂直于弦 于点
于点 ,
, 的延长线交
的延长线交 于点
于点 .若
.若 ,
, ,则
,则 的长是( )
的长是( )
| A.1 | B. | C.2 | D.4 |
11.如图,在平面直角坐标系xOy中,矩形OABC的顶点B的坐标为(10,4),四边形ABEF是菱形,且tan∠ABE=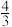 .若直线l把矩形OABC和菱形ABEF组成的图形的面积分成相等的两部分,则直线l的解析式为( )
.若直线l把矩形OABC和菱形ABEF组成的图形的面积分成相等的两部分,则直线l的解析式为( )

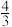 .若直线l把矩形OABC和菱形ABEF组成的图形的面积分成相等的两部分,则直线l的解析式为( )
.若直线l把矩形OABC和菱形ABEF组成的图形的面积分成相等的两部分,则直线l的解析式为( )
A. | B. |
C. | D. |
12.如图,在边长为3的正方形 中,点
中,点 是边
是边 上的点,且
上的点,且 ,过点
,过点 作
作 的垂线交正方形外角
的垂线交正方形外角 的平分线于点
的平分线于点 ,交边
,交边 于点
于点 ,连接
,连接 交边
交边 于点
于点 ,则
,则 的长为( )
的长为( )

 中,点
中,点 是边
是边 上的点,且
上的点,且 ,过点
,过点 作
作 的垂线交正方形外角
的垂线交正方形外角 的平分线于点
的平分线于点 ,交边
,交边 于点
于点 ,连接
,连接 交边
交边 于点
于点 ,则
,则 的长为( )
的长为( )
A. | B. | C. | D.1 |
13.点 关于原点的对称点的坐标为
关于原点的对称点的坐标为________ .
 关于原点的对称点的坐标为
关于原点的对称点的坐标为14.若 ,则
,则
________ .
 ,则
,则
15.若方程 的解使关于
的解使关于 的不等式
的不等式 成立,则实数
成立,则实数 的取值范围是
的取值范围是________ .
 的解使关于
的解使关于 的不等式
的不等式 成立,则实数
成立,则实数 的取值范围是
的取值范围是16.如图,在 中,
中, ,
, ,
, ,半径为1的
,半径为1的 在
在 内平移(
内平移( 可以与该三角形的边相切),则点
可以与该三角形的边相切),则点 到
到 上的点的距离的最大值为
上的点的距离的最大值为________ .

 中,
中, ,
, ,
, ,半径为1的
,半径为1的 在
在 内平移(
内平移( 可以与该三角形的边相切),则点
可以与该三角形的边相切),则点 到
到 上的点的距离的最大值为
上的点的距离的最大值为
17.计算: .
.
 .
.18.如图,已知点E、F分别在▱ABCD的边AB、CD上,且AE=CF.求证:DE=BF.


19.劳动教育具有树德、增智、强体、育美的综合育人价值,有利于学生树立正确的劳动价值观.某学校为了解学生参加家务劳动的情况,随机抽取了 名学生在某个休息日做家务的劳动时间作为样本,并绘制了以下不完整的频数分布表和扇形统计图.根据题中已有信息,解答下列问题:
名学生在某个休息日做家务的劳动时间作为样本,并绘制了以下不完整的频数分布表和扇形统计图.根据题中已有信息,解答下列问题:

(1) ________,
________, ________;
________;
(2)若该校学生有640人,试估计劳动时间在 范围的学生有多少人?
范围的学生有多少人?
(3)劳动时间在 范围的4名学生中有男生2名,女生2名,学校准备从中任意抽取2名交流劳动感受,求抽取的2名学生恰好是一名男生和一名女生的概率.
范围的4名学生中有男生2名,女生2名,学校准备从中任意抽取2名交流劳动感受,求抽取的2名学生恰好是一名男生和一名女生的概率.
 名学生在某个休息日做家务的劳动时间作为样本,并绘制了以下不完整的频数分布表和扇形统计图.根据题中已有信息,解答下列问题:
名学生在某个休息日做家务的劳动时间作为样本,并绘制了以下不完整的频数分布表和扇形统计图.根据题中已有信息,解答下列问题:劳动时间 (单位:小时) (单位:小时) | 频数 |
 | 12 |
 |  |
 | 28 |
 | 16 |
 | 4 |

(1)
 ________,
________, ________;
________;(2)若该校学生有640人,试估计劳动时间在
 范围的学生有多少人?
范围的学生有多少人?(3)劳动时间在
 范围的4名学生中有男生2名,女生2名,学校准备从中任意抽取2名交流劳动感受,求抽取的2名学生恰好是一名男生和一名女生的概率.
范围的4名学生中有男生2名,女生2名,学校准备从中任意抽取2名交流劳动感受,求抽取的2名学生恰好是一名男生和一名女生的概率.20.某经销商计划购进 ,
, 两种农产品.已知购进
两种农产品.已知购进 种农产品2件,
种农产品2件, 种农产品3件,共需690元;购进
种农产品3件,共需690元;购进 种农产品1件,
种农产品1件, 种农产品4件,共需720元.
种农产品4件,共需720元.
(1) ,
, 两种农产品每件的价格分别是多少元?
两种农产品每件的价格分别是多少元?
(2)该经销商计划用不超过5400元购进 ,
, 两种农产品共40件,且
两种农产品共40件,且 种农产品的件数不超过B种农产品件数的3倍.如果该经销商将购进的农产品按照
种农产品的件数不超过B种农产品件数的3倍.如果该经销商将购进的农产品按照 种每件160元,
种每件160元, 种每件200元的价格全部售出,那么购进
种每件200元的价格全部售出,那么购进 ,
, 两种农产品各多少件时获利最多?
两种农产品各多少件时获利最多?
 ,
, 两种农产品.已知购进
两种农产品.已知购进 种农产品2件,
种农产品2件, 种农产品3件,共需690元;购进
种农产品3件,共需690元;购进 种农产品1件,
种农产品1件, 种农产品4件,共需720元.
种农产品4件,共需720元.(1)
 ,
, 两种农产品每件的价格分别是多少元?
两种农产品每件的价格分别是多少元?(2)该经销商计划用不超过5400元购进
 ,
, 两种农产品共40件,且
两种农产品共40件,且 种农产品的件数不超过B种农产品件数的3倍.如果该经销商将购进的农产品按照
种农产品的件数不超过B种农产品件数的3倍.如果该经销商将购进的农产品按照 种每件160元,
种每件160元, 种每件200元的价格全部售出,那么购进
种每件200元的价格全部售出,那么购进 ,
, 两种农产品各多少件时获利最多?
两种农产品各多少件时获利最多?21.如图,直线 与反比例函数
与反比例函数 的图象相交于点
的图象相交于点 ,
, ,已知点
,已知点 的纵坐标为6
的纵坐标为6

(1)求 的值;
的值;
(2)若点 是
是 轴上一点,且
轴上一点,且 的面积为3,求点
的面积为3,求点 的坐标.
的坐标.
 与反比例函数
与反比例函数 的图象相交于点
的图象相交于点 ,
, ,已知点
,已知点 的纵坐标为6
的纵坐标为6
(1)求
 的值;
的值;(2)若点
 是
是 轴上一点,且
轴上一点,且 的面积为3,求点
的面积为3,求点 的坐标.
的坐标.22.如图,海中有两小岛C,D,某渔船在海中的A处测得小岛C位于东北方向,小岛D位于南偏东30°方向,且A,D相距10 nmile.该渔船自西向东航行一段时间后到达点B,此时测得小岛C位于西北方向且与点B相距8 nmile.求B,D间的距离(计算过程中的数据不取近似值).
nmile.求B,D间的距离(计算过程中的数据不取近似值).

 nmile.求B,D间的距离(计算过程中的数据不取近似值).
nmile.求B,D间的距离(计算过程中的数据不取近似值).
23.如图,点 在以
在以 为直径的
为直径的 上,
上, 平分
平分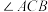 交
交 于点
于点 ,交
,交 于点
于点 ,过点
,过点 作
作 的切线交
的切线交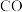 的延长线于点
的延长线于点 .
.

(1)求证: ;
;
(2)若 ,
, ,求
,求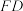 的长.
的长.
 在以
在以 为直径的
为直径的 上,
上, 平分
平分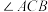 交
交 于点
于点 ,交
,交 于点
于点 ,过点
,过点 作
作 的切线交
的切线交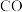 的延长线于点
的延长线于点 .
.
(1)求证:
 ;
;(2)若
 ,
, ,求
,求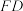 的长.
的长.24.如图,在平面直角坐标系 中,已知抛物线
中,已知抛物线 经过
经过 ,
, 两点,直线
两点,直线 与
与 轴交于点
轴交于点 .
.

(1)求 ,
, 的值;
的值;
(2)经过点 的直线分别与线段
的直线分别与线段 ,直线
,直线 交于点
交于点 ,
, ,且
,且 与
与 的面积相等,求直线
的面积相等,求直线 的解析式;
的解析式;
(3) 是抛物线上位于第一象限的一个动点,在线段
是抛物线上位于第一象限的一个动点,在线段 和直线
和直线 上是否分别存在点
上是否分别存在点 ,
, ,使
,使 ,
, ,
, ,
, 为顶点的四边形是以
为顶点的四边形是以 为一边的矩形?若存在,求出点
为一边的矩形?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 中,已知抛物线
中,已知抛物线 经过
经过 ,
, 两点,直线
两点,直线 与
与 轴交于点
轴交于点 .
.
(1)求
 ,
, 的值;
的值;(2)经过点
 的直线分别与线段
的直线分别与线段 ,直线
,直线 交于点
交于点 ,
, ,且
,且 与
与 的面积相等,求直线
的面积相等,求直线 的解析式;
的解析式;(3)
 是抛物线上位于第一象限的一个动点,在线段
是抛物线上位于第一象限的一个动点,在线段 和直线
和直线 上是否分别存在点
上是否分别存在点 ,
, ,使
,使 ,
, ,
, ,
, 为顶点的四边形是以
为顶点的四边形是以 为一边的矩形?若存在,求出点
为一边的矩形?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
