全一卷
1.-2022的绝对值是( )
| A.﹣2022 | B.2022 | C. | D. |
2.下列四种图形中,对称轴条数最多的是( )
| A.等边三角形 | B.圆 | C.长方形 | D.正方形 |
3.5月29日腾讯新闻报道,2022年第一季度,湖南全省地区生产总值约为11000亿元,11000亿用科学记数法可表示为 ,则
,则 的值是( )
的值是( )
 ,则
,则 的值是( )
的值是( )| A.0.11 | B.1.1 | C.11 | D.11000 |
4.下列四个图形中,圆柱体的俯视图是( )


A. | B. | C. | D. |
5.假定按同一种方式掷两枚均匀硬币,如果第一枚出现正面朝上,第二枚出现反面朝上,就记为(正,反),如此类推,出现(正,正)的概率是( )
| A.1 | B.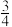 | C. | D.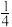 |
6.下列长度的三条线段能首尾相接构成三角形的是( )
A. , , , , | B. , , , , |
C. , , , , | D. , , , , |
7.如图是反比例函数y= 的图象,点A(x,y)是反比例函数图象上任意一点,过点A作AB⊥x轴于点B,连接OA,则△AOB的面积是( )
的图象,点A(x,y)是反比例函数图象上任意一点,过点A作AB⊥x轴于点B,连接OA,则△AOB的面积是( )

 的图象,点A(x,y)是反比例函数图象上任意一点,过点A作AB⊥x轴于点B,连接OA,则△AOB的面积是( )
的图象,点A(x,y)是反比例函数图象上任意一点,过点A作AB⊥x轴于点B,连接OA,则△AOB的面积是( )
| A.1 | B. | C.2 | D. |
8.在直角坐标系中,已知点 ,点
,点 是直线
是直线 上的两点,则
上的两点,则 ,
, 的大小关系是( )
的大小关系是( )
 ,点
,点 是直线
是直线 上的两点,则
上的两点,则 ,
, 的大小关系是( )
的大小关系是( )A. | B. | C. | D. |
9.如图,⊙O是等边△ABC的外接圆,若AB=3,则⊙O的半径是( )


A. | B. | C. | D. |
10.关于 的不等式组
的不等式组 有且只有三个整数解,则
有且只有三个整数解,则 的最大值是( )
的最大值是( )
 的不等式组
的不等式组 有且只有三个整数解,则
有且只有三个整数解,则 的最大值是( )
的最大值是( )| A.3 | B.4 | C.5 | D.6 |
11.因式分解: =
=_____ .
 =
=12.若 有意义,则
有意义,则 的取值范围是
的取值范围是_________ .
 有意义,则
有意义,则 的取值范围是
的取值范围是13.某班50名同学的身高(单位: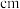 )如下表所示:
)如下表所示:
则该班同学的身高的众数为_________ .
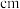 )如下表所示:
)如下表所示:身高 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 |
人数 | 3 | 5 | 1 | 2 | 2 | 10 | 4 | 3 | 1 | 2 | 6 | 8 | 1 | 2 |
则该班同学的身高的众数为
14.分式方程 的根为
的根为_____
 的根为
的根为15.已知矩形的一边长为 ,一条对角线的长为
,一条对角线的长为 ,则矩形的面积为
,则矩形的面积为_________  .
.
 ,一条对角线的长为
,一条对角线的长为 ,则矩形的面积为
,则矩形的面积为 .
.16.已知 ,则
,则
_________ .
 ,则
,则
17.如图,在等腰 中,
中, ,顶点
,顶点 在
在 的边
的边 上,已知
上,已知 ,则
,则
_________ .

 中,
中, ,顶点
,顶点 在
在 的边
的边 上,已知
上,已知 ,则
,则

18.如图,在 中,点
中,点 在
在 边上,点
边上,点 在
在 边上,请添加一个条件
边上,请添加一个条件_________ ,使 .
.

 中,点
中,点 在
在 边上,点
边上,点 在
在 边上,请添加一个条件
边上,请添加一个条件 .
.
19.计算: .
.
 .
.20.先化简,再从-1,0,1, 中选择一个合适的
中选择一个合适的 值代入求值.
值代入求值.
 .
.
 中选择一个合适的
中选择一个合适的 值代入求值.
值代入求值. .
.21.如图,在菱形 中,对角线
中,对角线 ,
, 相交于点
相交于点 ,点
,点 ,
, 在对角线
在对角线 上,且
上,且 ,
, .
.
求证:四边形 是正方形.
是正方形.

 中,对角线
中,对角线 ,
, 相交于点
相交于点 ,点
,点 ,
, 在对角线
在对角线 上,且
上,且 ,
, .
.求证:四边形
 是正方形.
是正方形.
22.2021年秋季,全国义务教育学校实现课后服务全覆盖.为了促进学生课后服务多样化,某校组织了第二课堂,分别设置了文艺类、体育类、阅读类、兴趣类四个社团(假设该校要求人人参与社团,每人只能选择一个).为了了解学生喜爱哪种社团活动,学校做了一次抽样调查,并绘制成如图(1)、图(2)所示的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题.

(1)求抽取参加调查的学生人数.
(2)将以上两幅不完整的统计图补充完整.
(3)若该校有1600人参加社团活动,试估计该校报兴趣类社团的学生人数.

(1)求抽取参加调查的学生人数.
(2)将以上两幅不完整的统计图补充完整.
(3)若该校有1600人参加社团活动,试估计该校报兴趣类社团的学生人数.
23.2022年2月4日至20日冬季奥运会在北京举行.某商店特购进冬奥会纪念品“冰墩墩”摆件和挂件共180个进行销售.已知“冰墩墩”摆件的进价为80元/个,“冰墩墩”挂件的进价为50元/个.
(1)若购进“冰墩墩”摆件和挂件共花费了11400元,请分别求出购进“冰墩墩”摆件和挂件的数量.
(2)该商店计划将“冰墩墩”摆件售价定为100元/个,“冰墩墩”挂件售价定为60元/个,若购进的180个“冰墩墩”摆件和挂件全部售完,且至少盈利2900元,求购进的“冰墩墩”挂件不能超过多少个?
(1)若购进“冰墩墩”摆件和挂件共花费了11400元,请分别求出购进“冰墩墩”摆件和挂件的数量.
(2)该商店计划将“冰墩墩”摆件售价定为100元/个,“冰墩墩”挂件售价定为60元/个,若购进的180个“冰墩墩”摆件和挂件全部售完,且至少盈利2900元,求购进的“冰墩墩”挂件不能超过多少个?
24.如图,已知 是
是 的直径,点
的直径,点 为
为 延长线上一点,
延长线上一点, 是
是 的切线,点
的切线,点 为切点,且
为切点,且 .
.

(1)求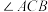 的度数;
的度数;
(2)若 的半径为3,求圆弧
的半径为3,求圆弧 的长.
的长.
 是
是 的直径,点
的直径,点 为
为 延长线上一点,
延长线上一点, 是
是 的切线,点
的切线,点 为切点,且
为切点,且 .
.
(1)求
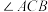 的度数;
的度数;(2)若
 的半径为3,求圆弧
的半径为3,求圆弧 的长.
的长.25.如图,一艘轮船从点 处以
处以 的速度向正东方向航行,在
的速度向正东方向航行,在 处测得灯塔
处测得灯塔 在北偏东
在北偏东 方向上,继续航行
方向上,继续航行 到达
到达 处,这时测得灯塔
处,这时测得灯塔 在北偏东
在北偏东 方向上,已知在灯塔
方向上,已知在灯塔 的四周
的四周 内有暗礁,问这艘轮船继续向正东方向航行是否安全?并说明理由.(提示:
内有暗礁,问这艘轮船继续向正东方向航行是否安全?并说明理由.(提示: ,
, )
)

 处以
处以 的速度向正东方向航行,在
的速度向正东方向航行,在 处测得灯塔
处测得灯塔 在北偏东
在北偏东 方向上,继续航行
方向上,继续航行 到达
到达 处,这时测得灯塔
处,这时测得灯塔 在北偏东
在北偏东 方向上,已知在灯塔
方向上,已知在灯塔 的四周
的四周 内有暗礁,问这艘轮船继续向正东方向航行是否安全?并说明理由.(提示:
内有暗礁,问这艘轮船继续向正东方向航行是否安全?并说明理由.(提示: ,
, )
)
26.如图,已知直线y=2x+2与抛物线y=ax2+bx+c相交于A,B两点,点A在x轴上,点B在y轴上,点C(3,0)在抛物线上.

(1)求该抛物线的表达式.
(2)正方形OPDE的顶点O为直角坐标系原点,顶点P在线段OC上,顶点E在y轴正半轴上,若△AOB与△DPC全等,求点P的坐标.
(3)在条件(2)下,点Q是线段CD上的动点(点Q不与点D重合),将△PQD沿PQ所在的直线翻折得到△PQD',连接CD',求线段CD'长度的最小值.

(1)求该抛物线的表达式.
(2)正方形OPDE的顶点O为直角坐标系原点,顶点P在线段OC上,顶点E在y轴正半轴上,若△AOB与△DPC全等,求点P的坐标.
(3)在条件(2)下,点Q是线段CD上的动点(点Q不与点D重合),将△PQD沿PQ所在的直线翻折得到△PQD',连接CD',求线段CD'长度的最小值.
 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
